题目内容
【题目】如图所示,已知直二面角α﹣AB﹣β,P∈α,Q∈β,PQ与平面α,β所成的角都为30°,PQ=4,PC⊥AB,C为垂足,QD⊥AB,D为垂足,求: 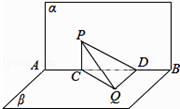
(1)直线PQ与CD所成角的大小
(2)四面体PCDQ的体积.
【答案】
(1)解:直二面角α﹣AB﹣β,P∈α,Q∈β,PQ与平面α,β所成的角都为30°,PQ=4,PC⊥AB,C为垂足,QD⊥AB,D为垂足,设直线AB与CD所成的角为θ,则由PC⊥AB,cos∠DCQ= ![]() =
= ![]() =
= ![]() ,
,
可知PC⊥β知:cosθ=cos∠PQCcos∠DCQ=cos30° ![]() =
= ![]() ,
,
故θ=45°
(2)解:由题意可知三棱锥的高为PC=2,底面CQD的面积为: ![]() CDDQ=
CDDQ= ![]() =2
=2 ![]() ,
,
三棱锥的体积为: ![]() =
= ![]()
【解析】(1)直接根据PC⊥β以及常用的结论:cosθ=cos∠PQCcos∠DCQ即可求出结果;(2)求出几何体的高与底面面积,即可求解几何体的体积.

练习册系列答案
相关题目
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量 ![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗 ![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
参考公式: 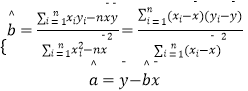
(1)已知产量 ![]() 和能耗
和能耗 ![]() 呈线性关系,请根据上表提供的数据,用最小二乘法求出
呈线性关系,请根据上表提供的数据,用最小二乘法求出 ![]() 关于
关于 ![]() 的线性回归方程
的线性回归方程 ![]() ;
;
(2)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?

