题目内容
3.数列{an}满足:a1+2a2+…nan=4-$\frac{n+2}{{2}^{n-1}}$,n∈N+.(1)求a3的值;
(2)求数列{an}的前 n项和Tn;
(3)令b1=a1,bn=$\frac{{T}_{n-1}}{n}$+(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)an(n≥2),证明:数列{bn}的前n项和Sn满足Sn<2+2lnn.
分析 (1)利用数列的递推关系即可求a3的值;
(2)利用作差法求出数列{an}的通项公式,利用等比数列的前n项和公式即可求数列{an}的前 n项和Tn;
(3)利用构造法,结合裂项法进行求解即可证明不等式.
解答 解:(1)∵a1+2a2+…nan=4-$\frac{n+2}{{2}^{n-1}}$,n∈N+.
∴a1=4-3=1,1+2a2=4-$\frac{2+2}{{2}^{2-1}}$=2,
解得a2=$\frac{1}{2}$,
∵a1+2a2+…+nan=4-$\frac{n+2}{{2}^{n-1}}$,n∈N+.
∴a1+2a2+…+(n-1)an-1=4-$\frac{n+1}{{2}^{n-2}}$,n∈N+.
两式相减得nan=4-$\frac{n+2}{{2}^{n-1}}$-(4-$\frac{n+1}{{2}^{n-2}}$)=$\frac{n}{{2}^{n-1}}$,n≥2,
则an=$\frac{1}{{2}^{n-1}}$,n≥2,
当n=1时,a1=1也满足,
∴an=$\frac{1}{{2}^{n-1}}$,n≥1,
则a3=$\frac{1}{{2}^{2}}=\frac{1}{4}$;
(2)∵an=$\frac{1}{{2}^{n-1}}$,n≥1,
∴数列{an}是公比q=$\frac{1}{2}$,
则数列{an}的前 n项和Tn=$\frac{1-(\frac{1}{2})^{n}}{1-\frac{1}{2}}$=2-21-n.
(3)bn=$\frac{{T}_{n-1}}{n}$+(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)an,
∴b1=a1,b2=$\frac{{a}_{1}}{2}$+(1+$\frac{1}{2}$)a2,b3=$\frac{{a}_{1}+{a}_{2}}{3}+$(1+$\frac{1}{2}$+$\frac{1}{3}$)a3,
∴bn=$\frac{{a}_{1}+{a}_{2}+…+{a}_{n-1}}{n}$+(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)an,
∴Sn=b1+b2+…+bn=(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)a1+(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)a2+…+(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)an
=(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)(a1+a2+…+an)=(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)Tn
=(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)(2-21-n)<2×(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$),
设f(x)=lnx+$\frac{1}{x}$-1,x>1,
则f′(x)=$\frac{1}{x}$-$\frac{1}{{x}^{2}}=\frac{x-1}{{x}^{2}}>0$.
即f(x)在(1,+∞)上为增函数,
∵f(1)=0,即f(x)>0,
∵k≥2,且k∈N•时,$\frac{k}{k-1}>1$,
∴f($\frac{k}{k-1}$)=ln$\frac{k}{k-1}$+$\frac{1}{\frac{k}{k-1}}$-1>0,即ln$\frac{k}{k-1}$>$\frac{1}{k}$,
∴$\frac{1}{2}<$ln$\frac{2}{1}$,$\frac{1}{3}<ln\frac{3}{2}$,…$\frac{1}{n}<ln\frac{n}{n-1}$,
即$\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n}<ln\frac{2}{1}+ln\frac{3}{2}+…+ln\frac{n}{n-1}$=lnn,
∴2×(1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)=2+2×($\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{n}$)<2+2lnn,
即Sn<2(1+lnn)=2+2lnn.
点评 本题主要考查数列通项公式以及前n项和的计算,以及数列和不等式的综合,利用作差法求出数列的通项公式是解决本题的关键.考查学生的计算能力,综合性较强,难度较大.

| A. | 200 | B. | 150 | C. | 100 | D. | 50 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | p1<p2<$\frac{1}{2}$ | B. | ${p_1}<\frac{1}{2}<{p_2}$ | C. | p2<$\frac{1}{2}<{p_1}$ | D. | $\frac{1}{2}<{p_2}<{p_1}$ |
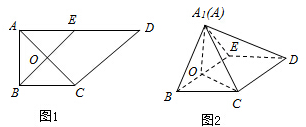 如图,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2.
如图,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点,将ABE沿BE折起到A1BE的位置,如图2.