题目内容
【题目】已知函数f(x)=|x-3|-|x+1|.
(1)求f(x)的值域;
(2)解不等式:f(x)>0;
(3)若直线y=a与f(x)的图像无交点,求实数a的取值范围.
【答案】(1) [-4,4] (2) (-∞,1) (3) a∈(-∞,-4)∪(4,+∞)
【解析】
(1)首先将函数的解析式写成分段函数的形式,然后求解其值域即可;
(2)结合函数的解析式零点分段求解不等式的解集即可;
(3)首先绘制函数f(x)的图像,然后数形结合即可确定实数a的取值范围.
若x≤-1,则x-3<0,x+1≤0,
f(x)=-(x-3)+(x+1)=4;
若-1<x≤3,则x-3≤0,x+1>0,
f(x)=-(x-3)-(x+1)=-2x+2;
若x>3,则x-3>0,x+1>0,
f(x)=(x-3)-(x+1)=-4.
∴f(x)=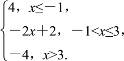
(1)-1<x≤3时,-4≤-2x+2<4.
∴f(x)的值域为[-4,4)∪{4}∪{-4}=[-4,4].
(2)f(x)>0,即![]() ①
①
或![]() ②
②
或![]() ③
③
解①得x≤-1,解②得-1<x<1,解③得x∈.
∴f(x)>0的解集为(-∞,-1]∪(-1,1)∪=(-∞,1).
(3)f(x)的图像如下:
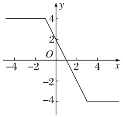
由图可知,当a∈(-∞,-4)∪(4,+∞)时,直线y=a与f(x)的图像无交点.

练习册系列答案
相关题目