题目内容
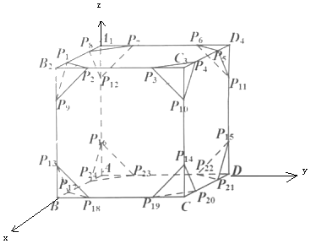
【题目】被嘉定著名学者钱大昕赞誉为“国朝算学第一”的清朝数学家梅文鼎曾创造出一类“方灯体”,“灯者立方去其八角也”,如图所示,在棱长为![]() 的正方体
的正方体![]() 中,点
中,点![]() 为棱上的四等分点.
为棱上的四等分点.

(1)求该方灯体的体积;
(2)求直线![]() 和
和![]() 的所成角;
的所成角;
(3)求直线![]() 和平面
和平面![]() 的所成角.
的所成角.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)计算出八个角(即八个三棱锥)的体积之和,然后利用正方体的体积减去这八个角的体积之和即可得出方灯体的体积;
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,利用空间向量法求出直线
轴,建立空间直角坐标系,利用空间向量法求出直线![]() 和
和![]() 的所成角;
的所成角;
(3)求出平面![]() 的法向量,利用空间向量法求出直线
的法向量,利用空间向量法求出直线![]() 和平面
和平面![]() 的所成角的正弦值,由此可得出
的所成角的正弦值,由此可得出![]() 和平面
和平面![]() 的所成角的大小.
的所成角的大小.
(1)![]() 在棱长为
在棱长为![]() 的正方体
的正方体![]() 中,点
中,点![]() 为棱上的四等分点,
为棱上的四等分点,
![]() 该方灯体的体积:
该方灯体的体积:![]() ;
;
(2)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
![]() 、
、![]() 、
、![]() 、
、![]() ,
,![]() ,
,![]() ,
,
设直线![]() 和
和![]() 的所成角为
的所成角为![]() ,则
,则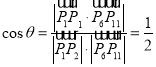 ,
,
![]() 直线
直线![]() 和
和![]() 的所成角为
的所成角为![]() ;
;
(3)![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则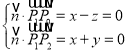 ,得
,得![]() ,取
,取![]() ,得
,得![]() ,
,
设直线![]() 和平面
和平面![]() 的所成角为
的所成角为![]() ,则
,则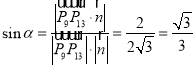 ,
,
![]() 直线
直线![]() 和平面
和平面![]() 的所成角为
的所成角为![]() .
.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
【题目】某学校高一、高二、高三的三个年级学生人数如下表
高三 | 高二 | 高一 | |
女生 | 100 | 150 | z |
男生 | 300 | 450 | 600 |
按年级分层抽样的方法评选优秀学生50人,其中高三有10人.
(1)求z的值;
(2)用分层抽样的方法在高一中抽取一个容量为5的样本,将该样本看成一个总体,从中任取2人,求至少有1名女生的概率;
(3)用随机抽样的方法从高二女生中抽取8人,经检测她们的得分如下:9.4,8.6,9.2, 9.6,8.7,9.3,9.0,8.2,把这8人的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
