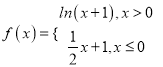Question

【题目】已知函数

（1）求函数的极值

（2）定义：若函数在区间 上的取值范围为，则称区间为函数的“美丽区间”．试问函数在上是否存在“美丽区间”？若存在，求出所有符合条件的“美丽区间”；若不存在，请说明理由

Answer 1

【答案】(1)当时，函数有极大值为1，当时，函数有极小值为．(2)见解析.

【解析】

（1）利用函数的正负性，来求原函数的单调区间，可得函数的极值；
（2）据“域同区间”的定义得到，则方程有两个大于3的相异实根．，然后利用方程根的情况列式求解，即可得出结论．

（1）因为，

所以 ．

令，可得或．

则在上的变化情况为：

		1		3
	+	0	－	0	+
	增函数	1	减函数		增函数

所以当时，函数有极大值为1，当时，函数有极小值为．

（2）假设函数在上存在“美丽区间” ，

由（1）知函数在上单调递增．

所以即

也就是方程有两个大于3的相异实根．

设 ，

则．

令 ，解得，．

当时， ，当时， ，

所以函数在区间上单调递减，在区间上单调递增．

因为，，，

所以函数在区间上只有一个零点．

这与方程有两个大于3的相异实根相矛盾，所以假设不成立．

所以函数在上不存在“美丽区间”．