题目内容
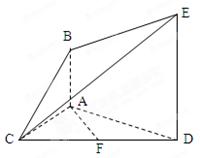
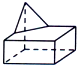
已知正△ABC的边长为 , CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
, CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
(1)试判断折叠后直线AB与平面DEF的位置关系,并说明理由;
(2)若棱锥E-DFC的体积为 ,求
,求 的值;
的值;
(3)在线段AC上是否存在一点P,使BP⊥DF?如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.

 , CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示.
, CD是AB边上的高,E、F分别是AC和BC边的中点,现将△ABC沿CD翻折成直二面角A-DC-B,如图所示. (1)试判断折叠后直线AB与平面DEF的位置关系,并说明理由;
(2)若棱锥E-DFC的体积为
 ,求
,求 的值;
的值;(3)在线段AC上是否存在一点P,使BP⊥DF?如果存在,求出
 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(1)平行; (2)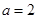 ; (3)存在AP:AC=1:3
; (3)存在AP:AC=1:3
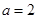 ; (3)存在AP:AC=1:3
; (3)存在AP:AC=1:3试题分析:(1)由于E、F分别是AC和BC边的中点,所以在翻折后的三角形ABC中,
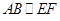 .由线面平行的判定定理可得结论.
.由线面平行的判定定理可得结论.(2)由棱锥E-DFC的体积为
 ,因为△ABC沿CD翻折成直二面角A-DC-B,并且
,因为△ABC沿CD翻折成直二面角A-DC-B,并且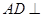 平面BCD,即由三棱锥的体积公式,即可求出结论.
平面BCD,即由三棱锥的体积公式,即可求出结论.(3)在线段AC上是否存在一点P,使BP⊥DF,即转化为直线与平面垂直的问题,假设存在点P作
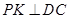 ,k为垂足,连结BK即可得到直线DF
,k为垂足,连结BK即可得到直线DF  平面BPK,所以可得
平面BPK,所以可得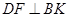 .通过三角形的相似即可得到所求的结论.
.通过三角形的相似即可得到所求的结论.(1)AB//平面DEF,
如图.在△ABC中,∵E,F分别是AC,BC的中点,故EF//AB,
又AB
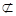 平面DEF,∴AB//平面DEF, 4分
平面DEF,∴AB//平面DEF, 4分(2)∵AD⊥CD,BD⊥CD, 将△ABC沿CD翻折成直二面角A-DC-B
∴AD⊥BD,AD⊥平面BCD,取CD中点M,则EM//AD,∴EM⊥平面BCD,且EM=a/2
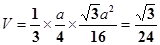 ,a="2." 8分
,a="2." 8分(3)存在满足条件的点P.
做法:因为三角形BDF为正三角形,过B做BK⊥DF,延长BK交DC于K,过K做KP//DA,交AC于P.则点P即为所求.
证明:∵AD⊥平面BCD , KP//DA,∴PK⊥平面BCD,PK⊥DF,又 BK⊥DF,PK∩BK=K,∴DF⊥平面PKB,DF⊥PB.又∠DBK=∠KBC=∠BCK=30°,∴DK=KF=KC/2.
故AP:OC=1:2,AP:AC=1:3 12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中, 平面
平面 .
.
 平面
平面 ;
; ,
,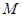 为
为 中点,求三棱锥
中点,求三棱锥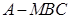 的体积.
的体积.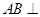 平面
平面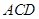 ,
,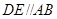 ,
,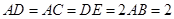 ,
,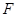 是
是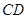 的中点,
的中点, .
. 平面
平面 ;
; 平面
平面 ;
;

 的五个顶点在同一球面上,若该正四棱锥的底面边长为2,侧棱长为
的五个顶点在同一球面上,若该正四棱锥的底面边长为2,侧棱长为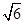 ,则这个球的表面积为_________.
,则这个球的表面积为_________. .
. 及其内部一动点
及其内部一动点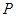 ,集合
,集合 ,则集合
,则集合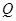 构成的几何体表面积为 .
构成的几何体表面积为 .