��Ŀ����
����Ŀ���ҹ�������������ȱˮ�Ĺ��ң�ij������Ϊ�˹��������Լ��ˮ���ƻ���������������ˮ�շѷ�������ȷ��һ������������ˮ����![]() ���֣���һλ���������ˮ��������
���֣���һλ���������ˮ��������![]() �IJ��ְ�ƽ���շѣ�����
�IJ��ְ�ƽ���շѣ�����![]() �IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���
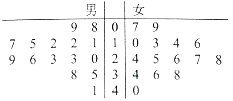
�IJ��ְ�����շѣ�Ϊ���˽������ˮ�����ͨ�������������ij��100λ����ÿ�˵��¾���ˮ������λ���֣��������ݰ���![]() ��
�� ![]() ������
������ ![]() �ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
�ֳ�9�飬�Ƴ�����ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
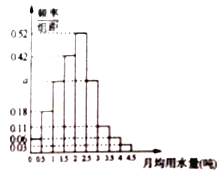
��1����ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2������Ƶ����Ϊ���ʣ��Ӹó��о����������ȡ3�ˣ�����3�����¾���ˮ��������3�ֵ�����Ϊ![]() ����
����![]() �ķֲ�������ѧ����.
�ķֲ�������ѧ����.
��3������������ϣ��ʹ85%�ľ���ÿ�µ���ˮ����������![]() ���֣�������
���֣�������![]() ��ֵ����ȷ��0.01������˵������.
��ֵ����ȷ��0.01������˵������.
���𰸡���1��![]() ��2����������3��
��2����������3��![]()
�����������������
(1)Ƶ�ʷֲ�ֱ��ͼ��С���������֮��Ϊ1���ݴ����![]() ��
��
(2)������ɵ�![]() ���ɶ���ֲ��������г��ֲ��У�Ȼ���������������Ϊ
���ɶ���ֲ��������г��ֲ��У�Ȼ���������������Ϊ![]()
(3)���Ƶ�ʷֲ�ֱ��ͼ�����ʽⷽ�̿ɵã� ![]() .
.
���������
�⣺
��1��![]()
![]()
��2��������Ӹó��о����г�ȡ��ˮ��������3�ֵĸ���Ϊ
![]()
��![]()
��![]()
![]()
| 0 | 1 | 2 | 3 |
| 0.729 | 0.243 | 0.027 | 0.001 |
![]()
��3������ˮ������3�ֵľ���ռ10%������![]()
![]() ��Ԫ��.
��Ԫ��.