题目内容
【题目】已知函数
.
（Ⅰ）讨论函数
的单调性；
（Ⅱ）或
， 
时，证明： 
.
【答案】（I）详见解析；（II）详见解析.
【解析】试题分析：（Ⅰ）函数的导数
，分
和
两种情况讨论函数的单调性；（Ⅱ）设
，设
，再求
，分
和
两种情况讨论函数的单调性和函数的最小值，证明函数的最小值大于0.
试题解析：（Ⅰ） 
的定义域为
， 
，
当
时， 
， 
，函数
单调递减；
当
时， 
， 
，函数
单调递减， 
， 
，函数
单调递增，
所以当
时，函数
在
单调递减；
当
时，函数
在
单调递减，在
单调递增.
（Ⅱ）设
， 
，
设
， 
.
①当
时， 
， 
，所以
在
上单调递增；
∴
，即
， 
在
上单调递增，
∴
，不等式成立；
②当
时， 
， 
； 
， 
，
所以
在
上单调递减，在
上单调递增；
∴
，
即
， 
在
上单调递增. ∴
，不等式成立；
综上所述：当
， 
时，有
恒成立.
练习册系列答案
相关题目
【题目】某公司2016年前三个月的利润（单位：百万元）如下：
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
（1）求利润
关于月份
的线性回归方程；
（2）试用（1）中求得的回归方程预测4月和5月的利润；
（3）试用（1）中求得的回归方程预测该公司2016年从几月份开始利润超过1000万？
相关公式：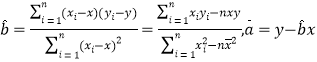
.
