Question

18．已知几何体的三视图如图所示，则该几何体的表面积为（　　）

• A． 4+$\sqrt{6}$
• B． 6+$\sqrt{6}$
• C． 2+2$\sqrt{2}$+$\sqrt{6}$
• D． 2+2$\sqrt{3}$+$\sqrt{6}$

Answer 1

分析 根据几何体的三视图，得出该几何体是侧面垂直于底面的三棱锥，结合图中数据，求出它的表面积．

解答 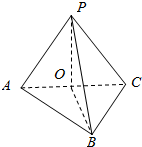解：根据几何体的三视图，得；
该几何体是如图所示的三棱锥，
且侧面PAC⊥底面ABC，
过点P作PO⊥AC，垂足为O，
则PO⊥平面ABC；
又PO=$\sqrt{3}$，AC=2$\sqrt{2}$，
∴S_△PAC=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$；
连接OB，则OB⊥AC，
又OB=$\sqrt{2}$，∴S_△ABC=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{2}$=2；
△PAB中，AB=$\sqrt{{（\sqrt{2}）}^{2}{+（\sqrt{2}）}^{2}}$=2，
PB=$\sqrt{{（\sqrt{2}）}^{2}{+（\sqrt{3}）}^{2}}$=$\sqrt{5}$，
PA=$\sqrt{{（\sqrt{2}）}^{2}{+（\sqrt{3}）}^{2}}$=$\sqrt{5}$
∴S_△PAB=$\frac{1}{2}$×2×$\sqrt{{（\sqrt{5}）}^{2}{-（\frac{2}{2}）}^{2}}$=2，
且S_△PBC=S_△PAB；
∴该几何体的表面积为S=S_△PAC+S_△ABC+2S_△PAB=$\sqrt{6}$+2+2×2=6+$\sqrt{6}$．
故选：B．

点评 本题考查了利用空间几何体的三视图求表面积的应用问题，是基础题目．