题目内容
4.设函数f(x)=$\left\{\begin{array}{l}{x}^{2}-4x+6,x≥0\\ x+6,x<0\end{array}\right.$则不等式f(x)>f(1)的解集是( )| A. | (-3,1)∪(3,+∞) | B. | (-3,1)∪(2,+∞) | C. | (-1,1)∪(3,+∞) | D. | (-∞,-1)∪(1,3) |
分析 求出函数值,利用分段函数求解不等式的解集即可.
解答 解:函数f(x)=$\left\{\begin{array}{l}{x}^{2}-4x+6,x≥0\\ x+6,x<0\end{array}\right.$,则f(1)=3,
不等式f(x)>f(1)等价于:$\left\{\begin{array}{l}x≥0\\{x}^{2}-4x+6>3\end{array}\right.$或$\left\{\begin{array}{l}x<0\\ x+6>3\end{array}\right.$,
解得:x∈(-3,1)∪(3,+∞).
故选:A.
点评 本题考查分段函数的应用,不等式组的解法,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
根据上表可得回归直线方程$\hat y=\hat bx+\hat a$,其中$\hat b=0.76,\hat a=\overline y-\hat b\overline x$,据此估计,该社区一户收入为15万元家庭年支出为( )
| 收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
| A. | 11.4万元 | B. | 11.8万元 | C. | 12.0万元 | D. | 12.2万元 |
15.已知等比数列{an}的前n项和为Sn,若S2n=4(a1+a3+…+a2n-1),a1•a2•a3=27,则a6=( )
| A. | 27 | B. | 81 | C. | 243 | D. | 729 |
13.已知圆C:x2+y2-4x-4y=0与x轴相交于A,B两点,则弦AB所对的圆心角的大小( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
 如图,已知抛物线C1:y=$\frac{1}{4}$x2,圆C2:x2+(y-1)2=1,过点P(t,0)(t>0)作不过原点O的直线PA,PB分别与抛物线C1和圆C2相切,A,B为切点.
如图,已知抛物线C1:y=$\frac{1}{4}$x2,圆C2:x2+(y-1)2=1,过点P(t,0)(t>0)作不过原点O的直线PA,PB分别与抛物线C1和圆C2相切,A,B为切点.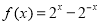 ,数列
,数列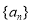 满足
满足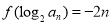 .
.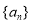 的通项公式;
的通项公式;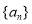 是递减数列.
是递减数列.