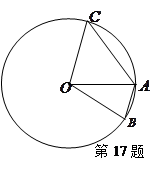题目内容
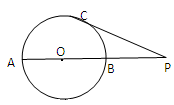
如图,AB是圆O的直径,P是AB延长线上的一点,过P作圆O的切线,切点为C,PC=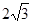 若
若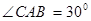 ,则圆O的直径AB等于( )
,则圆O的直径AB等于( )
 .
.
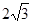 若
若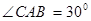 ,则圆O的直径AB等于( )
,则圆O的直径AB等于( ) .
.| A.2 | B.4 | C.6 | D.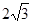 |
B
解:连接BC,设圆的直径是x则三角形ABC是一个含有30°角的三角形,
∴BC=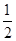 AB,三角形BPC是一个等腰三角形,BC=BP=
AB,三角形BPC是一个等腰三角形,BC=BP=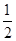 AB,∵PC是圆的切线,PA是圆的割线,∴PC2=PB•PC=
AB,∵PC是圆的切线,PA是圆的割线,∴PC2=PB•PC=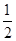 x•
x•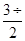 x=
x=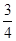 x2,∵PC=
x2,∵PC=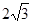 ,∴x=4,故答案为B
,∴x=4,故答案为B
∴BC=
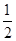 AB,三角形BPC是一个等腰三角形,BC=BP=
AB,三角形BPC是一个等腰三角形,BC=BP=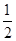 AB,∵PC是圆的切线,PA是圆的割线,∴PC2=PB•PC=
AB,∵PC是圆的切线,PA是圆的割线,∴PC2=PB•PC=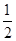 x•
x•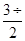 x=
x=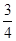 x2,∵PC=
x2,∵PC=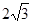 ,∴x=4,故答案为B
,∴x=4,故答案为B
练习册系列答案
相关题目
 是△
是△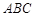 的外接圆,D是的中点,BD交AC于E.
的外接圆,D是的中点,BD交AC于E.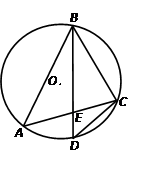
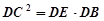 ;
;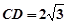 ,O到AC的距离为1,求⊙O的半径
,O到AC的距离为1,求⊙O的半径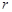 .
.
 ,AB="BC=4," 则AC的长为
,AB="BC=4," 则AC的长为 
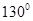 ,则
,则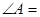 ( )
( )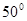
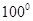
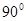
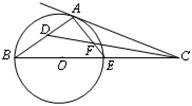
 的度数;
的度数;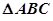 是圆O的内接三角形,圆O的半径
是圆O的内接三角形,圆O的半径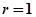 ,
,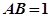 ,
,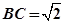 ,
,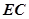 是圆
是圆 的切线,则
的切线,则 _______.
_______.
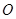 为△
为△ 的外心,
的外心, 为钝角,
为钝角, 是边
是边 的中点,则
的中点,则 的值 ( ).
的值 ( ).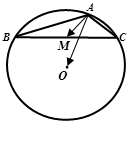
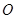 的半径为
的半径为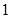 ,点
,点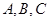 是⊙
是⊙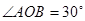 ,
,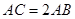 ,则
,则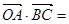 _____________.
_____________.