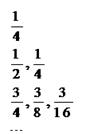题目内容
已知等差数列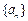 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列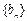 的首项为b,公比为a,其中a,b都是大于1的正整数,且
的首项为b,公比为a,其中a,b都是大于1的正整数,且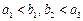 .
.
(1)求a的值;
(2)若对于任意的 ,总存在
,总存在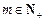 ,使得
,使得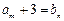 成立,求b的值;
成立,求b的值;
(3)令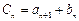 ,问数列
,问数列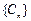 中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
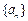 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列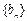 的首项为b,公比为a,其中a,b都是大于1的正整数,且
的首项为b,公比为a,其中a,b都是大于1的正整数,且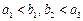 .
.(1)求a的值;
(2)若对于任意的
 ,总存在
,总存在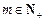 ,使得
,使得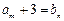 成立,求b的值;
成立,求b的值;(3)令
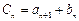 ,问数列
,问数列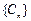 中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.(1)2(2)5(3)当 时,不存在连续三项成等比数列;当
时,不存在连续三项成等比数列;当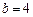 时,数列
时,数列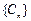 中的第二、三、四项成等比数列,这三项依次是18,30,50.
中的第二、三、四项成等比数列,这三项依次是18,30,50.
 时,不存在连续三项成等比数列;当
时,不存在连续三项成等比数列;当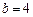 时,数列
时,数列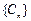 中的第二、三、四项成等比数列,这三项依次是18,30,50.
中的第二、三、四项成等比数列,这三项依次是18,30,50.(1)由已知,得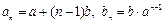 .由
.由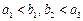 ,得
,得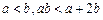 .
.
因a,b都为大于1的正整数,故a≥2.又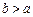 ,故b≥3.再由
,故b≥3.再由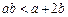 ,得
,得 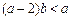 .
.
由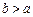 ,故
,故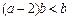 ,即
,即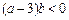 .
.
由b≥3,故 ,解得
,解得 . 于是
. 于是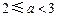 ,根据
,根据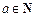 ,可得
,可得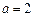 .
.
(2)由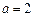 ,对于任意的
,对于任意的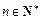 ,均存在
,均存在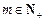 ,使得
,使得 ,则
,则
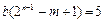 .
.
又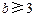 ,由数的整除性,得b是5的约数.
,由数的整除性,得b是5的约数.
故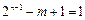 ,b=5.
,b=5.
所以b=5时,存在正自然数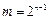 满足题意.
满足题意.
(3)设数列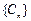 中,
中, 成等比数列,由
成等比数列,由 ,
,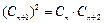 ,得
,得
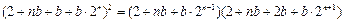 .
.
化简,得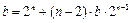 . (※)
. (※)
当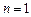 时,
时, 时,等式(※)成立,而
时,等式(※)成立,而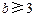 ,不成立.
,不成立.
当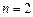 时,
时,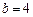 时,等式(※)成立.当
时,等式(※)成立.当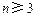 时,
时, ,这与b≥3矛盾.
,这与b≥3矛盾.
这时等式(※)不成立.
综上所述,当 时,不存在连续三项成等比数列;当
时,不存在连续三项成等比数列;当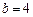 时,数列
时,数列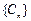 中的第二、三、四项成等比数列,这三项依次是18,30,50.
中的第二、三、四项成等比数列,这三项依次是18,30,50.
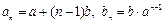 .由
.由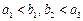 ,得
,得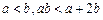 .
.因a,b都为大于1的正整数,故a≥2.又
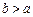 ,故b≥3.再由
,故b≥3.再由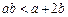 ,得
,得 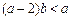 .
.由
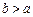 ,故
,故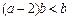 ,即
,即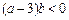 .
.由b≥3,故
 ,解得
,解得 . 于是
. 于是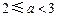 ,根据
,根据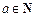 ,可得
,可得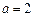 .
.(2)由
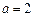 ,对于任意的
,对于任意的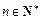 ,均存在
,均存在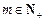 ,使得
,使得 ,则
,则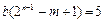 .
.又
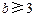 ,由数的整除性,得b是5的约数.
,由数的整除性,得b是5的约数.故
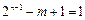 ,b=5.
,b=5.所以b=5时,存在正自然数
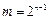 满足题意.
满足题意.(3)设数列
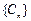 中,
中, 成等比数列,由
成等比数列,由 ,
,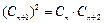 ,得
,得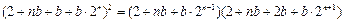 .
.化简,得
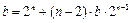 . (※)
. (※) 当
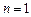 时,
时, 时,等式(※)成立,而
时,等式(※)成立,而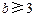 ,不成立.
,不成立.当
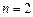 时,
时,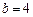 时,等式(※)成立.当
时,等式(※)成立.当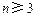 时,
时, ,这与b≥3矛盾.
,这与b≥3矛盾.这时等式(※)不成立.
综上所述,当
 时,不存在连续三项成等比数列;当
时,不存在连续三项成等比数列;当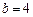 时,数列
时,数列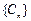 中的第二、三、四项成等比数列,这三项依次是18,30,50.
中的第二、三、四项成等比数列,这三项依次是18,30,50.
练习册系列答案
相关题目
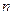 为正整数时,区间
为正整数时,区间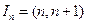 ,
,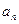 表示函数
表示函数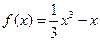 在
在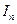 上函数值取整数值的个数,当
上函数值取整数值的个数,当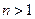 时,记
时,记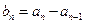 .当
.当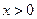 ,
,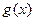 表示把
表示把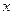 “四舍五入”到个位的近似值,如
“四舍五入”到个位的近似值,如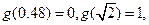
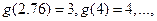 当
当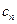 表示满足
表示满足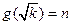 的正整数
的正整数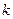 的个数.
的个数.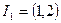 的单调性;
的单调性;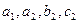 ;
;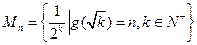 中所有元素之和为
中所有元素之和为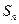 ,记
,记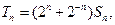 求证:
求证: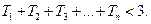
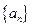 满足递推关系
满足递推关系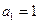 且
且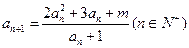 .
.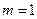 时,求数列
时,求数列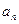 ;(2) 当
;(2) 当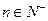 时,数列
时,数列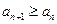 恒成立,求
恒成立,求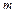 的取值范围;(3) 在
的取值范围;(3) 在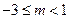 时,证明:
时,证明: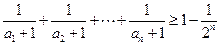 .
.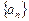 中,其中
中,其中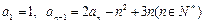
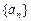 的通项公式;
的通项公式;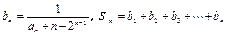 ,证明:当
,证明:当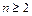 时,
时,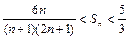 .
. (x≥4)的反函数为
(x≥4)的反函数为 ,数列
,数列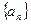 满足:a1=1,
满足:a1=1, ,(
,( N*),数列
N*),数列 ,
, ,
, ,…,
,…, 是首项为1,公比为
是首项为1,公比为 的等比数列.
的等比数列. ,求数列
,求数列 的前n项和
的前n项和 .
.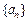 中,公差d > 0,其前n项和为
中,公差d > 0,其前n项和为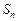 ,且满足
,且满足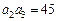 ,
,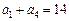 ,
,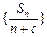 为等差数列.
为等差数列.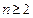 时,其前n项和满足
时,其前n项和满足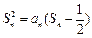
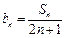 ,数列{bn}的前n项和为Tn,求Tn.
,数列{bn}的前n项和为Tn,求Tn.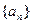 是等差数列,
是等差数列,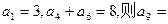 .
.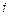 行第
行第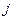 列的数为
列的数为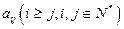 ,则
,则