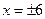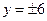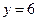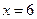题目内容
已知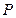 点在以坐标轴为对称轴的椭圆上,点
点在以坐标轴为对称轴的椭圆上,点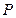 到两个焦点的距离分别为
到两个焦点的距离分别为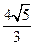 和
和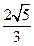 ,过
,过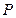 作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程。
作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程。
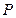 点在以坐标轴为对称轴的椭圆上,点
点在以坐标轴为对称轴的椭圆上,点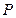 到两个焦点的距离分别为
到两个焦点的距离分别为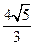 和
和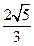 ,过
,过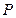 作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程。
作焦点所在轴的垂线恰好过椭圆的一个焦点,求椭圆的方程。椭圆的方程为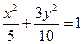 或
或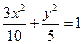
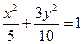 或
或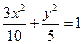
设两焦点为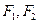 ,且
,且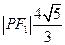 ,
, ,由椭圆的定义知:
,由椭圆的定义知: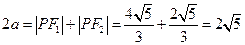 ,∴
,∴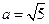 。∵
。∵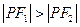 ,∴由题意知
,∴由题意知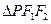 为直角三角形,在
为直角三角形,在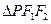 中,
中,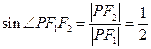 ,∴
,∴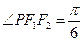 ,∴
,∴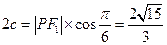 ,∴
,∴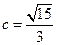 ,∴
,∴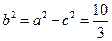 。因为焦点可以在
。因为焦点可以在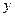 轴上,也可能在
轴上,也可能在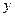 轴上,∴椭圆的方程为
轴上,∴椭圆的方程为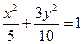 或
或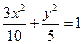 。
。
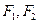 ,且
,且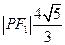 ,
, ,由椭圆的定义知:
,由椭圆的定义知: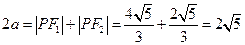 ,∴
,∴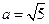 。∵
。∵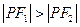 ,∴由题意知
,∴由题意知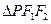 为直角三角形,在
为直角三角形,在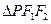 中,
中,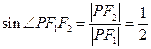 ,∴
,∴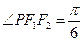 ,∴
,∴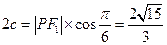 ,∴
,∴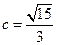 ,∴
,∴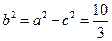 。因为焦点可以在
。因为焦点可以在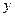 轴上,也可能在
轴上,也可能在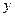 轴上,∴椭圆的方程为
轴上,∴椭圆的方程为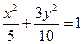 或
或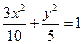 。
。
练习册系列答案
相关题目
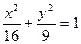 ,点A、B是它的两个焦点,当静止的小球放在点A处,从点A沿直线出发,经椭圆壁反弹后,再回到点A时,小球经过的最短路程是( ).
,点A、B是它的两个焦点,当静止的小球放在点A处,从点A沿直线出发,经椭圆壁反弹后,再回到点A时,小球经过的最短路程是( ).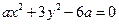 的一个焦点坐标为
的一个焦点坐标为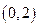 ,求
,求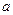 的值。
的值。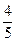 ,长轴长为
,长轴长为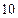 ,在椭圆上有一点
,在椭圆上有一点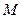 到左准线的距离为
到左准线的距离为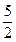 ,求点
,求点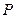 是椭圆
是椭圆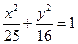 上的一点,
上的一点,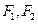 是焦点,若
是焦点,若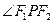 是直角,则
是直角,则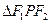 的面积为 。
的面积为 。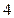 ,与圆柱底面成
,与圆柱底面成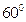 角的平面截这个圆柱得到一个椭圆,则这个椭圆的离心率为 。
角的平面截这个圆柱得到一个椭圆,则这个椭圆的离心率为 。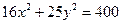 的长轴长和短轴长、离心率、焦点和顶点坐标及准线方程。
的长轴长和短轴长、离心率、焦点和顶点坐标及准线方程。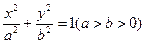 的左、右准线分别为
的左、右准线分别为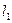 、
、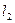 ,且分别交
,且分别交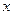 轴于
轴于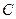 、
、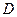 两点,从
两点,从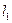 上一点
上一点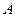 发出一条光线经过椭圆的左焦点
发出一条光线经过椭圆的左焦点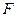 被
被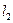 交于点
交于点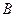 ,若
,若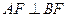 ,且
,且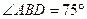 ,则椭圆的离心率等于( )
,则椭圆的离心率等于( )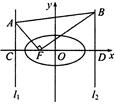
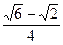
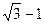

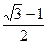
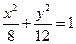 的准线方程是( )
的准线方程是( )