题目内容
在等比数列{an}中,an>0(n∈N*),且a1a3=4,a3+1是a2和a4的等差中项.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an+1+log2an(n=1,2,3,…),求数列{bn}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=an+1+log2an(n=1,2,3,…),求数列{bn}的前n项和Sn.
(1)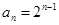 ;(2)
;(2)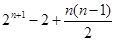 .
.
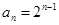 ;(2)
;(2)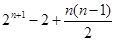 .
.试题分析:(1)设出等比数列的基本量
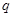 ,利用条件得出关于
,利用条件得出关于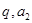 的方程组,解得即可;(2)由(1)得出数列
的方程组,解得即可;(2)由(1)得出数列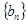 是由等比数列与等差数列相加得到,因此利用分组法求和.
是由等比数列与等差数列相加得到,因此利用分组法求和.规律总结:涉及等差数列或等比数列的通项问题,往往列出关于基本量的方程组,进而求出基本量;数列求和的方法主要有:倒序相加法、分组求和、错位相减法、裂项抵消法..
试题解析:(1)设等比数列{an}的公比为q.由a1a3=4可得

因为an>0,所以a2=2, 依题意有a2+a4=2(a3+1),得2a3=a4=a3q
因为a3>0,所以q=2, 所以数列{an}的通项公式为an=2n-1.
(2)bn=an+1+log2an=2n+n-1,
可得Sn=(2+22+23+…+2n)+[1+2+3+…+(n-1)]=
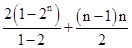
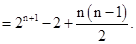

练习册系列答案
相关题目
 的公差为3,若
的公差为3,若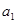 ,
,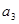 ,
,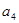 成等比数列,则
成等比数列,则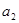 = .
= .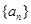 为等差数列,若
为等差数列,若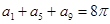 ,则
,则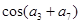 的值为 _____________.
的值为 _____________.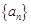 为等差数列,首项
为等差数列,首项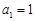 ,公差
,公差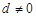 ,若
,若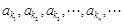 成等比数列,且
成等比数列,且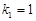 ,
,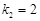 ,
,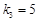 ,则
,则 .
.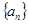 为等差数列,若
为等差数列,若 ,且它们的前n项和
,且它们的前n项和 有最大值,
有最大值, 的n的最大值为( ).
的n的最大值为( ).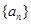 的前n项和
的前n项和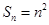 ,则
,则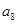 的值为( ).
的值为( ).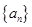 ,
,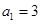 ,
,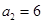 ,且
,且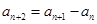 ,则数列的第五项为( )
,则数列的第五项为( )