题目内容
已知数列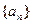 的各项均为正数,其前
的各项均为正数,其前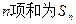 ,且
,且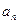 与1的等差中项等于
与1的等差中项等于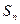 与
与
1的等比中项。
(1)求数列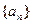 的通项公式;
的通项公式;
(2)设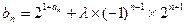 ,且数列
,且数列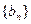 是单调递增数列。试求实数
是单调递增数列。试求实数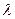 的取值范围。
的取值范围。
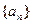 的各项均为正数,其前
的各项均为正数,其前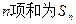 ,且
,且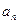 与1的等差中项等于
与1的等差中项等于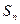 与
与1的等比中项。
(1)求数列
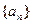 的通项公式;
的通项公式;(2)设
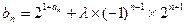 ,且数列
,且数列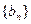 是单调递增数列。试求实数
是单调递增数列。试求实数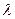 的取值范围。
的取值范围。(1)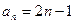 ; (2)
; (2)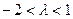
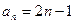 ; (2)
; (2)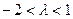
(1)由已知得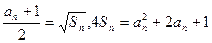 ……………………2分
……………………2分
当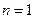 时代入得
时代入得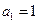 …………………………3分
…………………………3分
当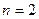 时
时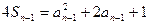 ,
,
所以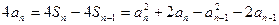 ……………………4分
……………………4分
整理得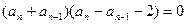 ,
,
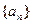 的各项均为正数,
的各项均为正数,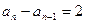 …………………………5分
…………………………5分
又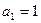 ,所以
,所以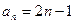 …………………………6分
…………………………6分
(2)由(1)得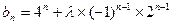
又数列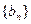 是单调增数列,
是单调增数列,
所以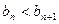 恒成立,
恒成立,
从而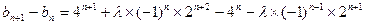
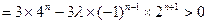 恒成立
恒成立
所以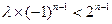 恒成立……………………10分
恒成立……………………10分
(I)当n是奇数时得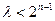 恒成立,
恒成立,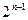 最小值为1,
最小值为1,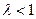
(Ⅱ)当n是偶数时得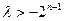 恒成立,
恒成立,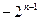 最大值为-2,
最大值为-2,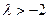
综上得: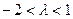 ……………………12分
……………………12分
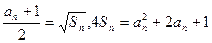 ……………………2分
……………………2分当
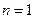 时代入得
时代入得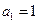 …………………………3分
…………………………3分当
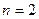 时
时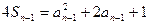 ,
,所以
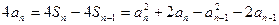 ……………………4分
……………………4分整理得
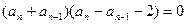 ,
,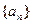 的各项均为正数,
的各项均为正数,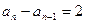 …………………………5分
…………………………5分又
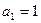 ,所以
,所以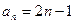 …………………………6分
…………………………6分(2)由(1)得
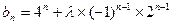
又数列
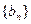 是单调增数列,
是单调增数列,所以
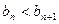 恒成立,
恒成立,从而
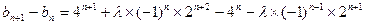
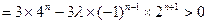 恒成立
恒成立所以
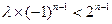 恒成立……………………10分
恒成立……………………10分(I)当n是奇数时得
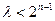 恒成立,
恒成立,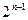 最小值为1,
最小值为1,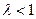
(Ⅱ)当n是偶数时得
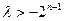 恒成立,
恒成立,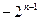 最大值为-2,
最大值为-2,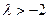
综上得:
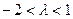 ……………………12分
……………………12分
练习册系列答案
相关题目
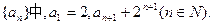
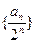 为等差数列;(II)若m为正整数,当
为等差数列;(II)若m为正整数,当
 }的首项a
}的首项a =1,前n项和S
=1,前n项和S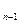 =3t(t>0,n=2,3,4…).(1)求证:数列{a
=3t(t>0,n=2,3,4…).(1)求证:数列{a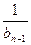 )(n=2,3,4…),求
)(n=2,3,4…),求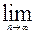
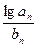 ;(3) 对于(2)中的数列{b
;(3) 对于(2)中的数列{b -b
-b +b
+b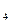 -…+(-1)
-…+(-1)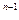 b
b 的和。
的和。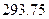 m?
m?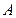 、
、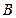 两种菜可供选择.调查资料表明,凡是在这星期一选
两种菜可供选择.调查资料表明,凡是在这星期一选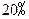 改选
改选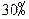 改选
改选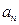 ,
,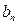 分别表示在第
分别表示在第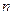 个星期选
个星期选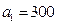 ,求
,求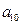
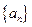 的前
的前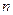 项和为
项和为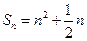 ,求这个数列的通项公式.这个数列是等差数列吗?如果是,它的首项与公差分别是什么?
,求这个数列的通项公式.这个数列是等差数列吗?如果是,它的首项与公差分别是什么? ,且
,且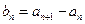 ,若
,若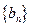 构成公差为
构成公差为 的等差数列.
的等差数列.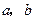 和
和 表示
表示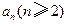 ;
;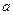 是满足
是满足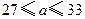 的整数,则当
的整数,则当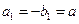 时,数列
时,数列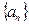 满足
满足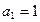 ,
,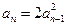 (n≥2).求数列
(n≥2).求数列