题目内容
【题目】已知函数![]() , 则: (1)曲线
, 则: (1)曲线![]() 的斜率为
的斜率为![]() 的切线方程为__________;
的切线方程为__________;
(2)设![]() ,记
,记![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() .当
.当![]() 最小时,
最小时,![]() 的值为__________.
的值为__________.
【答案】![]() 与
与![]() -3
-3
【解析】
(1)先求导,根据导数几何意义求出切线的斜率,再结合点斜式求出方程即可
(2)令![]() ,结合导数求得
,结合导数求得![]() ,再令
,再令![]() ,则
,则![]() ,
,![]() ,结合绝对值函数的对称性,进一步讨论参数
,结合绝对值函数的对称性,进一步讨论参数![]() 与-3的关系即可求解
与-3的关系即可求解
(1) 由![]() 得
得![]() ,
,
令![]() ,即
,即![]() ,得
,得![]() 或
或![]()
又![]()
所以曲线![]() 的斜率为
的斜率为![]() 的切线方程是
的切线方程是![]() 与
与![]()
即![]() 与
与![]()
(2)令![]() .
.
由![]() 得
得![]() ,
,
令![]() 得
得![]() 或/span>
或/span>![]()
![]() 的情况如表:
的情况如表:
|
|
|
|
|
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
所以![]() 的最小值为
的最小值为![]() ,最大值为
,最大值为![]() ,可令
,可令![]() ,则
,则![]() ,
,![]() ,此时根据绝对值函数的对称性进行分类讨论,
,此时根据绝对值函数的对称性进行分类讨论,
当![]() 时,即
时,即![]() 时,如图:
时,如图:

函数![]() 的对称轴为
的对称轴为![]() ,此时
,此时![]() ;
;
当![]() 时,即
时,即![]() 时,如图:
时,如图:
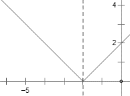
![]() ,当
,当![]() 时,
时,![]() ;
;
当![]() 时,即
时,即![]() 时,如图:
时,如图:
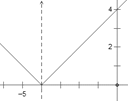
![]() ,当
,当![]() 时,
时,![]() ;
;
综上所述,当![]() 最小时,
最小时,![]() 的值为-3
的值为-3

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案
相关题目