题目内容
【题目】如图,四棱锥P﹣ABCD中,△PAD为正三角形,AB∥CD,AB=2CD,∠BAD=90°,PA⊥CD,E为棱PB的中点
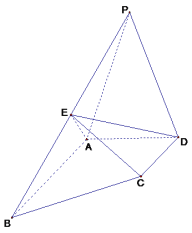
(1)求证:平面PAB⊥平面CDE;
(2)若AD=CD=2,求点P到平面ADE的距离.
【答案】(1)证明见解析;(2) ![]()
【解析】
(1)要证明面面垂直,需证明线面垂直,取AP的中点F,连结EF,DF,根据题中所给的条件证明![]() ,即证明
,即证明![]() 平面
平面![]() ;
;
(2)利用等体积![]() ,根据所给的条件,易求
,根据所给的条件,易求![]() ,点
,点![]() 到平面
到平面![]() 的距离就是
的距离就是![]() ,并且根据点,线,面的关系和边长求
,并且根据点,线,面的关系和边长求![]() 的面积.
的面积.
证明:(1)取AP的中点F,连结EF,DF,
∵E是PB中点,∴EF∥AB,EF=![]() AB,
AB,
又CD∥AB,CD=![]() AB, ∴CD∥EF,CD=EF
AB, ∴CD∥EF,CD=EF
∴四边形CDEF为平行四边形,
∴DF∥CE,
又△PAD 为正三角形,
∴PA⊥DF,从而PA⊥CE,
又PA⊥CD,CD∩CE=C,
∴PA⊥平面CDE,
又PA平面PAB,
∴平面PAB⊥平面CDE.
⑵∵AB∥CD,AB⊥AD,
∴CD⊥AD,
又PA⊥CD,PA∩AD=A,
∴CD⊥平面PAD,
又(1)知,CD∥EF,∴EF⊥平面PAD,
∴EF为三棱锥的E﹣PAD的高,且EF=CD=2,
易得△PAD的面积S△PAD=![]() ×22=
×22=![]() ,
,
在Rt△PAB中,PB=2![]() ,AE=
,AE=![]() PB=
PB=![]() ,
,
在矩形CDEF中,CD=2,CE=DF=![]() ,∴DE=
,∴DE=![]()
在△ADE中,AE=![]() ,DE=
,DE=![]() ,AD=2,
,AD=2,
![]()
![]()
∴△ADE的面积![]() ,
,
设点P到平面ADE的距离为d,由VP﹣ADE=VE﹣PAD得
![]() ×
×![]() ×2=
×2=![]() ×
×![]() d,
d,
解得d=![]() ∴点P到平面ADE的距离为
∴点P到平面ADE的距离为![]()

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目