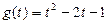题目内容
设f(x)=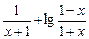 .
.
(1)证明:f(x)在其定义域上的单调性;
(2)证明: 方程f-1(x)=0有惟一解;
(3)解不等式f[x(x- )]<
)]< .
.
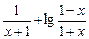 .
. (1)证明:f(x)在其定义域上的单调性;
(2)证明: 方程f-1(x)=0有惟一解;
(3)解不等式f[x(x-
 )]<
)]< .
. (1) 证明略(2)证明略(3)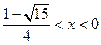 或
或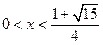
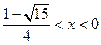 或
或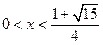
由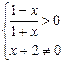 得f(x)的定义域为(-1,1),
得f(x)的定义域为(-1,1),
易判断f(x)在(-1,1)内是减函数.
(2)证明:∵f(0)= ,∴f--1(
,∴f--1( )=0,即x=
)=0,即x= 是方程f--1(x)=0的一个解.
是方程f--1(x)=0的一个解.
若方程f--1(x)=0还有另一个解x0≠ ,则f--1(x0)=0,
,则f--1(x0)=0,
由反函数的定义知f(0)=x0≠ ,与已知矛盾,故方程f--1(x)=0有惟一解
,与已知矛盾,故方程f--1(x)=0有惟一解
(3)解: f[x(x- )]<
)]< ,即f[x(x-
,即f[x(x- )]<f(0).
)]<f(0).
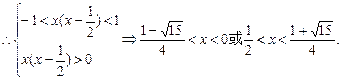
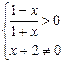 得f(x)的定义域为(-1,1),
得f(x)的定义域为(-1,1),易判断f(x)在(-1,1)内是减函数.
(2)证明:∵f(0)=
 ,∴f--1(
,∴f--1( )=0,即x=
)=0,即x= 是方程f--1(x)=0的一个解.
是方程f--1(x)=0的一个解.若方程f--1(x)=0还有另一个解x0≠
 ,则f--1(x0)=0,
,则f--1(x0)=0,由反函数的定义知f(0)=x0≠
 ,与已知矛盾,故方程f--1(x)=0有惟一解
,与已知矛盾,故方程f--1(x)=0有惟一解
(3)解: f[x(x-
 )]<
)]< ,即f[x(x-
,即f[x(x- )]<f(0).
)]<f(0). 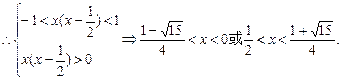

练习册系列答案
相关题目
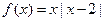 (1)画出函数的图像,写出
(1)画出函数的图像,写出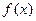 的单调区间;
的单调区间;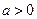 ,求
,求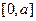 上的最大值
上的最大值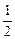 ],都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0.
],都有f(x1+x2)=f(x1)·f(x2),且f(1)=a>0. 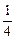 );
);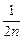 ),求
),求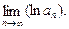



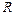 上的函数
上的函数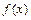 的图象关于点
的图象关于点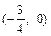 成中心对称,对任意的实数
成中心对称,对任意的实数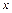 都有
都有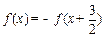 ,且
,且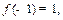
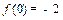 ,则
,则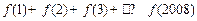 的值为
的值为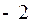
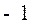
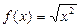 ,
,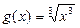 ;
;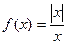 ,
,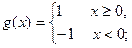
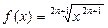 ,
,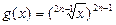 (n∈N*);
(n∈N*);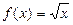
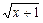 ,
,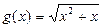 ;
;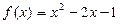 ,
,