题目内容
已知数列{an}满足an+1= (n∈N*),且a1=
(n∈N*),且a1= .
.
(1)求证:数列 是等差数列,并求an.
是等差数列,并求an.
(2)令bn= (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn.
 (n∈N*),且a1=
(n∈N*),且a1= .
.(1)求证:数列
 是等差数列,并求an.
是等差数列,并求an.(2)令bn=
 (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn. (1)an= (2)Tn=
(2)Tn= -
-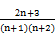 .
.
 (2)Tn=
(2)Tn= -
-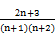 .
.(1)因为an+1= ,
,
所以an+1-1= -1=
-1= ,
,
故 =
= =
= +
+
=- +
+ ,
,
所以 -
- =-
=- ,
,
所以数列 是公差为-
是公差为- 的等差数列,
的等差数列,
而a1= ,所以
,所以 =
= =-
=- ,
,
所以 =-
=- -
- (n-1)=-
(n-1)=- ,
,
所以an-1=- ,an=1-
,an=1- =
= .
.
(2)由(1)知an= ,
,
所以bn= =
= =
= -
- ,
,
故Tn=b1+b2+…+bn
= -
- +
+ -
- +…+
+…+ -
-
=1+ -
- -
-
= -
-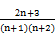 .
.
 ,
,所以an+1-1=
 -1=
-1= ,
,故
 =
= =
= +
+
=-
 +
+ ,
,所以
 -
- =-
=- ,
,所以数列
 是公差为-
是公差为- 的等差数列,
的等差数列,而a1=
 ,所以
,所以 =
= =-
=- ,
,所以
 =-
=- -
- (n-1)=-
(n-1)=- ,
,所以an-1=-
 ,an=1-
,an=1- =
= .
.(2)由(1)知an=
 ,
,所以bn=
 =
= =
= -
- ,
,故Tn=b1+b2+…+bn
=
 -
- +
+ -
- +…+
+…+ -
-
=1+
 -
- -
-
=
 -
-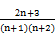 .
.
练习册系列答案
相关题目
 满足
满足 ,
, .
. 的值,由此猜测
的值,由此猜测 .
. 和
和 的通项公式分别为
的通项公式分别为 ,
, .将
.将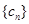 .
. ,
, ,
, ,
, 的值,并由此归纳数列
的值,并由此归纳数列 .
. 是首项
是首项 ,公比为
,公比为 的等比数列,
的等比数列,

 =2
=2 2+λ
2+λ 是一个等差数列且
是一个等差数列且 ,
, ,
, 项和
项和 的最小值.
的最小值.