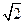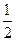题目内容
(2011•重庆)设实数数列{an}的前n项和Sn满足Sn+1=an+1Sn(n∈N*).
(1)若a1,S2,﹣2a2成等比数列,求S2和a3.
(2)求证:对k≥3有0≤ak≤ .
.
(1)若a1,S2,﹣2a2成等比数列,求S2和a3.
(2)求证:对k≥3有0≤ak≤
 .
.(1)S2=﹣2 
(2)见解析

(2)见解析
(1)由题意 ,
,
得S22=﹣2S2,
由S2是等比中项知S2≠0,
∴S2=﹣2.
由S2+a3=a3S2,解得 .
.
(2)证明:因为Sn+1=a1+a2+a3+…+an+an+1=an+1+Sn,
由题设条件知Sn+an+1=an+1Sn,
∴Sn≠1,an+1≠1,且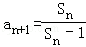 ,
,
从而对k≥3 有ak=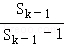 =
= =
= ①
①
因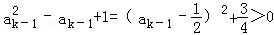 ,且
,且 ,
,
要证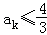 ,由①,只要证
,由①,只要证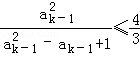
即证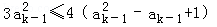 ,即
,即 ,
,
此式明显成立,因此 .
.
 ,
,得S22=﹣2S2,
由S2是等比中项知S2≠0,
∴S2=﹣2.
由S2+a3=a3S2,解得
 .
.(2)证明:因为Sn+1=a1+a2+a3+…+an+an+1=an+1+Sn,
由题设条件知Sn+an+1=an+1Sn,
∴Sn≠1,an+1≠1,且
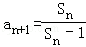 ,
,
从而对k≥3 有ak=
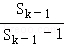 =
= =
= ①
①因
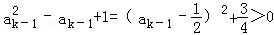 ,且
,且 ,
,要证
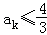 ,由①,只要证
,由①,只要证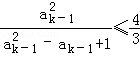
即证
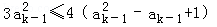 ,即
,即 ,
,此式明显成立,因此
 .
.
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 中,其前
中,其前 项和为
项和为 ,且
,且 .
. 是数列
是数列 的前
的前 是数列
是数列 的前
的前 .
. 的各项均为正数,记
的各项均为正数,记 ,
,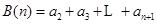 ,
, .
.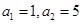 ,且对任意
,且对任意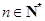 ,三个数
,三个数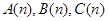 组成等差数列,求数列
组成等差数列,求数列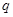 的等比数列的充分必要条件是:对任意
的等比数列的充分必要条件是:对任意

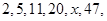 …中的
…中的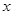 等于( )
等于( )


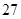
 (n∈N*),且a1=
(n∈N*),且a1= .
. 是等差数列,并求an.
是等差数列,并求an. (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn.  满足:
满足: ,且前
,且前 项和
项和 ,则
,则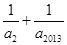 的最小值为________.
的最小值为________.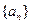 是公差不为0的等差数列,且
是公差不为0的等差数列,且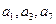 为等比数列
为等比数列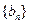 的连续三项,则数列
的连续三项,则数列