题目内容
已知数列 满足
满足 ,
, .
.
(1)求 的值,由此猜测
的值,由此猜测 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;
(2)证明: .
.
 满足
满足 ,
, .
.(1)求
 的值,由此猜测
的值,由此猜测 的通项公式,并证明你的结论;
的通项公式,并证明你的结论;(2)证明:
 .
.(1)猜想 ,证明详见解析;(2)证明详见解析.
,证明详见解析;(2)证明详见解析.
 ,证明详见解析;(2)证明详见解析.
,证明详见解析;(2)证明详见解析.试题分析:(1)根据递推关系,依次附值
 即可得到
即可得到 的取值,进而作出猜想
的取值,进而作出猜想 ,然后再用数学归纳法证明即可;(2)先化简
,然后再用数学归纳法证明即可;(2)先化简 ,进而采用放缩法得到
,进而采用放缩法得到 ,进而将
,进而将 取1,2,3,……,
取1,2,3,……, 时的不等式相乘即可证明不等式
时的不等式相乘即可证明不等式 ,然后构造函数
,然后构造函数 ,确定该函数在区间
,确定该函数在区间 上的单调性,进而得到
上的单调性,进而得到 在
在 恒成立,从而可得
恒成立,从而可得 即
即 ,问题得以证明.
,问题得以证明.(1)令
 可知
可知 ,
, ,
,
猜想
 ,下用数学归纳法证明.
,下用数学归纳法证明.(1)
 时,显然成立;
时,显然成立;(2)假设
 时,命题成立.即
时,命题成立.即 .
.当
 时,由题可知
时,由题可知 .
.故
 时,命题也成立.
时,命题也成立.由(1)(2)可知,
 .
.(2)证明:∵



∴

由于
 ,可令函数
,可令函数 ,则
,则 ,令
,令 ,得
,得 ,给定区间
,给定区间 ,则有
,则有 ,则函数
,则函数 在
在 上单调递减,∴
上单调递减,∴ ,即
,即 在
在 恒成立,又
恒成立,又 ,则有
,则有 ,即
,即
所以
 .
.
练习册系列答案
相关题目
 }是等比数列.
}是等比数列. 中,其前
中,其前 项和为
项和为 ,且
,且 .
. 是数列
是数列 的前
的前 是数列
是数列 的前
的前 .
. 所表示的平面区域为
所表示的平面区域为 ,记
,记
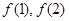 的值及
的值及 的表达式;
的表达式; 为数列
为数列 的前
的前 项的和,其中
项的和,其中 ,问是否存在正整数
,问是否存在正整数 ,使
,使 成立?若存在,求出正整数
成立?若存在,求出正整数

 (n∈N*),且a1=
(n∈N*),且a1= .
. 是等差数列,并求an.
是等差数列,并求an. (n∈N*),求数列{bn}的前n项和Tn.
(n∈N*),求数列{bn}的前n项和Tn. 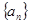 满足
满足 (
( 为常数),则称数列
为常数),则称数列 ,
, ,则
,则 ( )
( ) 

 为等差数列
为等差数列 的前
的前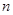 项和,若
项和,若 ,公差
,公差 ,
, ,则
,则 ( )
( )


