��Ŀ����
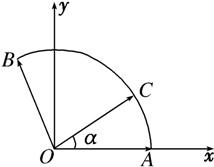
11�� ��ͼ����������ƽ������$\overrightarrow{{O}{A}}$��$\overrightarrow{{O}{B}}$�����ǵļн�Ϊ120�㣬��C����OΪԲ�ĵ�Բ��AB�ϣ���$\overrightarrow{{O}C}=x\overrightarrow{{O}{A}}+y\overrightarrow{{O}{B}}$������x��y��R����������y-x��$\frac{{\sqrt{3}}}{3}$�ĸ���Ϊ��������
��ͼ����������ƽ������$\overrightarrow{{O}{A}}$��$\overrightarrow{{O}{B}}$�����ǵļн�Ϊ120�㣬��C����OΪԲ�ĵ�Բ��AB�ϣ���$\overrightarrow{{O}C}=x\overrightarrow{{O}{A}}+y\overrightarrow{{O}{B}}$������x��y��R����������y-x��$\frac{{\sqrt{3}}}{3}$�ĸ���Ϊ��������| A�� | $\frac{��}{4}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{1}{3}$ | D�� | $\frac{1}{4}$ |
���� �������⣬��������ϵ�����A��B������꣬�����AOC=��������$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$��x��y��ֵ���Ӷ����y-x�ı���ʽ��������Һ��������ʿ������������ĽǦ��ķ�Χ�����ü��θ��͵ĸ��ʹ�ʽ���ɵõ����ۣ�
��� �⣺������ͼ��ʾ������ϵ��
��A��1��0����B��cos120�㣬sin120�㣩����B��-$\frac{1}{2}$��$\frac{\sqrt{3}}{2}$����
���AOC=������$\overrightarrow{OC}$=��cos����sin����
��$\overrightarrow{OC}$=x$\overrightarrow{OA}$+y$\overrightarrow{OB}$=��x��0��+��-$\frac{1}{2}y$��$\frac{\sqrt{3}}{2}y$��=��cos����sin������
�� $\left\{\begin{array}{l}{x-\frac{1}{2}y=cos��}\\{\frac{\sqrt{3}y}{2}=sin��}\end{array}\right.$����$\left\{\begin{array}{l}{x=\frac{sin��}{\sqrt{3}}+cos��}\\{y=\frac{2sin��}{\sqrt{3}}}\end{array}\right.$��
$\left\{\begin{array}{l}{x-\frac{1}{2}y=cos��}\\{\frac{\sqrt{3}y}{2}=sin��}\end{array}\right.$����$\left\{\begin{array}{l}{x=\frac{sin��}{\sqrt{3}}+cos��}\\{y=\frac{2sin��}{\sqrt{3}}}\end{array}\right.$��
��y-x=$\frac{2sin��}{\sqrt{3}}$-$\frac{sin��}{\sqrt{3}}$-cos��=$\frac{sin��}{\sqrt{3}}$-cos��=$\frac{\sqrt{3}}{3}$sin��-cos��=$\frac{2\sqrt{3}}{3}$��$\frac{1}{2}$sin��-$\frac{\sqrt{3}}{2}$cos����=$\frac{2\sqrt{3}}{3}$sin����-60�㣩��
��0��ܦ���120�㣮
��-60��ܦ�-60���60�㣮
��y-x��$\frac{{\sqrt{3}}}{3}$�ģ���$\frac{2\sqrt{3}}{3}$sin����-60�㣩��$\frac{{\sqrt{3}}}{3}$��
��sin����-60�㣩��$\frac{1}{2}$��
��30��ܦ�-60���60�㣬
��90��ܦ���120�㣬
������y-x��$\frac{{\sqrt{3}}}{3}$�ĸ���P=$\frac{120��-90��}{120��}$=$\frac{30}{120}$=$\frac{1}{4}$��
��ѡ��D
���� ������Ҫ���鼸�θ��͵ļ��㣬�������Ǻ����Ķ�Ӧת��Ϊ�Ƕ�֮��Ĺ�ϵ�ǽ������Ĺؼ��������ۺ��Խ�ǿ���ѶȽϴ�

| A�� | $\frac{1}{2}$ | B�� | $\frac{1}{4}$ | C�� | $\frac{1}{2e}$ | D�� | $\frac{1}{4e}$ |
| �Ŷ������� | 0�� | 1�� | 2�� | 3�� | 4�� | 5�˼�5������ |
| ���� | 0.05 | 0.14 | 0.35 | 0.3 | 0.1 | 0.06 |
��1��������2�˵Ⱥ��Ŷӵĸ����Ƕ��٣�
��2��������3�˵Ⱥ��Ŷӵĸ����Ƕ��٣�
| A�� | ��-$\frac{9}{4}$��0] | B�� | [-$\frac{9}{4}$��0] | C�� | ��-�ޣ�-$\frac{9}{4}$����[0��+�ޣ� | D�� | ��-�ޣ�-$\frac{9}{4}$]�ȣ�0��+�ޣ� |