题目内容
16.已知函数f(x)=$\left\{\begin{array}{l}{-{x}^{2}+1(x<1)}\\{\frac{lnx}{x}(x≥1)}\end{array}\right.$,参数k∈[-1,1],则方程f(x)-kx=0有四个实数根的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2e}$ | D. | $\frac{1}{4e}$ |
分析 画出函数f(x)的图象,要使方程f(x)-kx=0有四个实数根,只要函数f(x)与直线y=kx由四个交点即可,利用数形结合求k的范围以及导数进行求解,然后利用几何概型公式求概率.
解答 解:函数f(x)的图形如图,要使方程f(x)-kx=0有四个实数根,
即使直线y=kx与函数f(x)图象有四个交点,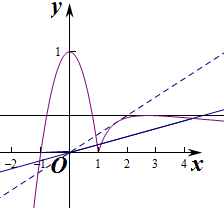
当直线y=kx与f(x)相切时,
设切线斜率为k,(k>0),切点为(m,n),
则刚x≥1时,f′(x)=$\frac{1-lnx}{{x}^{2}}$,
则k=f′(m)=$\frac{1-lnm}{{m}^{2}}$,
则对应的切线方程为y-n=$\frac{1-lnm}{{m}^{2}}$(x-m),
即y=$\frac{1-lnm}{{m}^{2}}$x-$\frac{1-lnm}{m}$+$\frac{lnm}{m}$,
∵切线方程为y=kx,
则k=$\frac{1-lnm}{{m}^{2}}$,-$\frac{1-lnm}{m}$+$\frac{lnm}{m}$=0,
即2lnm=1,解得m=$\sqrt{e}$,
此时k=$\frac{1-lnm}{{m}^{2}}$=$\frac{1-ln\sqrt{e}}{e}$=$\frac{1}{2e}$,
则方程f(x)-kx=0有四个实的k的范围是(0,$\frac{1}{2e}$),
又k∈[-1,1],由几何概型的公式可得方程f(x)-kx=0有四个实数根的概率为P=$\frac{\frac{1}{2e}}{2}=\frac{1}{4e}$;
故选D.
点评 本题考查几何概型的概率公式的应用,方程根的个数,利用导数求切线斜率;利用数形结合是解决本题的关键.,综合性较强难度较大.

练习册系列答案
相关题目
11. 如图,给定两个平面向量$\overrightarrow{{O}{A}}$和$\overrightarrow{{O}{B}}$,它们的夹角为120°,点C在以O为圆心的圆弧AB上,且$\overrightarrow{{O}C}=x\overrightarrow{{O}{A}}+y\overrightarrow{{O}{B}}$(其中x,y∈R),则满足y-x≥$\frac{{\sqrt{3}}}{3}$的概率为( )
如图,给定两个平面向量$\overrightarrow{{O}{A}}$和$\overrightarrow{{O}{B}}$,它们的夹角为120°,点C在以O为圆心的圆弧AB上,且$\overrightarrow{{O}C}=x\overrightarrow{{O}{A}}+y\overrightarrow{{O}{B}}$(其中x,y∈R),则满足y-x≥$\frac{{\sqrt{3}}}{3}$的概率为( )
 如图,给定两个平面向量$\overrightarrow{{O}{A}}$和$\overrightarrow{{O}{B}}$,它们的夹角为120°,点C在以O为圆心的圆弧AB上,且$\overrightarrow{{O}C}=x\overrightarrow{{O}{A}}+y\overrightarrow{{O}{B}}$(其中x,y∈R),则满足y-x≥$\frac{{\sqrt{3}}}{3}$的概率为( )
如图,给定两个平面向量$\overrightarrow{{O}{A}}$和$\overrightarrow{{O}{B}}$,它们的夹角为120°,点C在以O为圆心的圆弧AB上,且$\overrightarrow{{O}C}=x\overrightarrow{{O}{A}}+y\overrightarrow{{O}{B}}$(其中x,y∈R),则满足y-x≥$\frac{{\sqrt{3}}}{3}$的概率为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
1.直线Ax+By=0的系数A,B可以在0,1,2,3,5,7这六个数字中选取,则这些方程所表示的不同直线有( )
| A. | 30条 | B. | 23条 | C. | 22条 | D. | 14条 |