题目内容
2．函数f（x）=ax2-x是R上的减函数，则（ ）| A． | a=0 | B． | a＜1 | C． | a＜0 | D． | a≤1 |
分析 函数f（x）=ax2-x在R上的减函数，函数为一次函数，则a=0．
解答 解：∵函数f（x）=ax2-x在R上的减函数，
∴a=0，
故选：A．
点评 本题考查函数的单调性，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
12．定义在R上的函数y=f（x），满足f（x+2）=-$\frac{1}{f（x）}$，则（ ）
| A． | f（x）不是周期函数 | B． | f（x）是周期函数，且最小正周期为2 | ||
| C． | f（x）是周期函数，且最小正周期为4 | D． | f（x）是周期函数，且4是它的一个周期 |
10．已知$\overrightarrow{a}$=（m-1，1），$\overrightarrow{b}$=（-n-1，2），其中m＞0，n＞0，若存在实数λ使$\overrightarrow{b}=λ\overrightarrow{a}$，则$\frac{1}{m}$+$\frac{2}{n}$的最小值是（ ）
| A． | 2$\sqrt{2}$ | B． | 4 | C． | 4$\sqrt{2}$ | D． | 8 |
5．用数学归纳法证明$\frac{1}{n+1}+\frac{1}{n+2}+…+\frac{1}{2n}＞\frac{13}{24}$，由n=k到n=k+1左边需添加的项为（ ）
| A． | $\frac{1}{2（k+1）}$ | B． | $\frac{1}{2k+1}+\frac{1}{2k+2}-\frac{1}{k+1}$ | ||
| C． | $\frac{1}{2k+1}+\frac{1}{2k+2}+\frac{1}{k+1}$ | D． | $\frac{1}{2k+1}+\frac{1}{2k+2}$ |
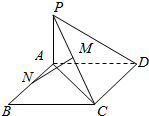如图：ABCD为矩形，PA⊥平面ABCD，PA=AD=1，AB=2，M、N分别是PC、AB中点，请选择适当的坐标系证明：MN⊥平面PCD．