题目内容
13.已知等差数列{an}中,公差d≠0,a2是a1与a4的等比中项,且a4-a1=6,在等比数列{bn}中,公比q>0,且b1=a1,b3=a4.(1)求数列{an}和{bn}的通项公式;
(2)设Cn=$\frac{1}{2n({a}_{n}+2)}$,数列{Cn}的前n项和为Tn.若Tn>$\frac{1}{8}$(1-m2)对n∈N*恒成立,求实数m的取值范围.
分析 (1)利用等差数列与等比数列的通项公式即可得出;
(2)利用“裂项求和”与不等式的性质即可得出.
解答 解:(1)∵a2是a1与a4的等比中项,且a4-a1=6,
∴${a}_{2}^{2}={a}_{1}{a}_{4}$即$({a}_{1}+d)^{2}={a}_{1}•({a}_{1}+3d)$,3d=6,
解得d=2,a1=2,
∴an=2+2(n-1)=2n.
在等比数列{bn}中,公比q>0,且b1=a1,b3=a4.
∴b1=2,b3=8=2q2,解得q=2.
∴bn=2n.
(2)Cn=$\frac{1}{2n({a}_{n}+2)}$=$\frac{1}{2n(2n+2)}$=$\frac{1}{4}(\frac{1}{n}-\frac{1}{n+1})$.
∴数列{Cn}的前n项和为Tn=$\frac{1}{4}$$[(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})$+…+$(\frac{1}{n}-\frac{1}{n+1})]$=$\frac{1}{4}(1-\frac{1}{n+1})$,
∵Tn>$\frac{1}{8}$(1-m2)对n∈N*恒成立,
∴$\frac{1}{4}×\frac{1}{2}$>$\frac{1}{8}$(1-m2),m2>0,
∴实数m的取值范围是(-∞,0)∪(0,+∞).
点评 本题考查了等差数列与等比数列的通项公式、“裂项求和”与不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
3.已知$\overrightarrow{OA}$=$\overrightarrow{i}+3\overrightarrow{k}$,$\overrightarrow{OB}$=$\overrightarrow{j}+3\overrightarrow{k}$,则△OAB的面积为( )
| A. | $\frac{\sqrt{19}}{2}$ | B. | 2$\sqrt{19}$ | C. | $\sqrt{19}$ | D. | 8$\sqrt{19}$ |
1.某程序框图如图所示,该程序运行后输出的S的值是( )
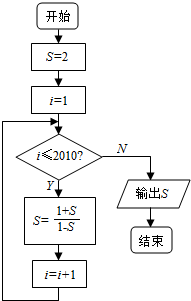

| A. | 2 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{2}$ |
18.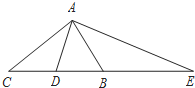 在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
 在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )
在△ABC中,∠BAC=90°,D是BC边的中点,AE⊥AD,AE交CB的延长线于E,则下面结论中正确的是( )| A. | △AED∽△ACB | B. | △AEB∽△ACD | C. | △BAE∽△ACE | D. | △AEC∽△DAC |
2.设随机变量x~N(1,δ2),若P(x>2)=0.3,则P(x>0)等于( )
| A. | 0.3 | B. | 0.4 | C. | 0.6 | D. | 0.7 |
3.复数z=i2+i3(i是虚数单位)在复平面中对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |