题目内容
函数
在
内有极小值，则实数
的取值范围为（ ）
A． | B． | C． | D． |
D
解析试题分析：对于函数
，求导可得
，∵函数在（0，1）内有极小值，∴，则其有一根在（0，1）内，a＞0时，3x2-2a=0两根为±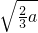
，若有一根在（0，1）内，则0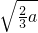＜＜1，即0＜a＜
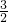．a=0时，3x2-3a=0两根相等，均为0，f（x）在（0，1）内无极小值．a＜0时，3x2-3a=0无根，f（x）在（0，1）内无极小值，综合可得，0＜a＜．
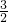考点：考查利用导数研究函数的极值问题，体现了转化的思想方法．
练习册系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知曲线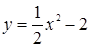
上一点P（1，
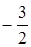），则过点P的切线的倾斜角为（ ）
| A．30° | B．45° | C．135° | D．165° |
曲线
与直线
所围成的封闭图形的面积为( )
A． | B． | C． | D． |
设函数
是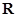
上以4为周期的可导偶函数，则曲线
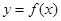在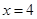
处的切线的斜率为（ ）
A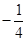． | B． | C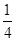． | D．4 |
曲线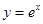
在点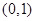
处的切线斜率为（ ）
A． | B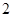． | C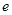． | D． |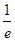
函数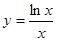
的最大值为（ ）
A． | B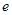． | C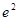． | D． |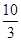
函数f(x)＝ex－x(e为自然对数的底数)在区间[－1,1]上的最大值是( )
A．1＋ | B．1 | C．e＋1 | D．e－1 |
（2011•湖北）放射性元素由于不断有原子放射出微粒子而变成其他元素，其含量不断减少，这种现象称为衰变．假设在放射性同位素铯137的衰变过程中，其含量M（单位：太贝克）与时间t（单位：年）满足函数关系：M（t）=M0
，其中M0为t=0时铯137的含量．已知t=30时，铯137含量的变化率是﹣10In2（太贝克/年），则M（60）=（ ）
| A．5太贝克 | B．75In2太贝克 | C．150In2太贝克 | D．150太贝克 |
如果函数y=f（x）的图象如图，那么导函数y=f′（x）的图象可能是（ ）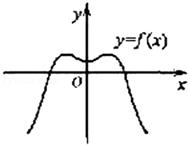
 |  |  |  |
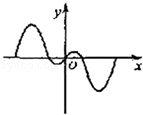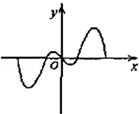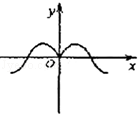| A． | B． | C． | D． |