题目内容
已知曲线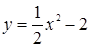 上一点P(1,
上一点P(1,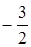 ),则过点P的切线的倾斜角为( )
),则过点P的切线的倾斜角为( )
| A.30° | B.45° | C.135° | D.165° |
B
解析试题分析: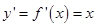 ,所以
,所以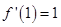 。由导数的几何意义可得在点
。由导数的几何意义可得在点 处切线的斜率为1,设此切线的倾斜角为
处切线的斜率为1,设此切线的倾斜角为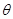 ,即
,即 ,因为
,因为 ,所以
,所以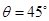 。故B正确。
。故B正确。
考点:1导数的几何意义;2斜率的定义。

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
由直线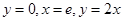 及曲线
及曲线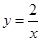 所围成的封闭的图形的面积为( )
所围成的封闭的图形的面积为( )
A.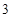 | B.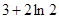 | C.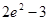 | D.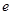 |
设函数 在
在 上可导,则
上可导,则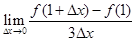 等于( )
等于( )
A.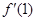 | B.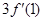 | C.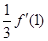 | D.以上都不对 |
二项式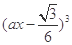 (
(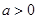 )的展开式的第二项的系数为
)的展开式的第二项的系数为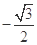 ,则
,则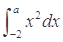 的值为( )
的值为( )
A. | B.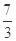 | C. 或 或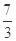 | D. 或 或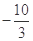 |
已知f(x)=x3+x,若a,b,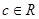 ,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )
,且a+b>0,a+c>0,b+c>0,则f(a)+f(b)+f(c)的值( )
| A.一定大于0 | B.一定等于0 |
| C.一定小于0 | D.正负都有可能 |
已知函数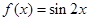 ,则
,则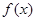 的导函数
的导函数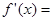 ( )
( )
A.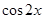 | B.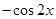 | C.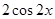 | D.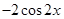 |
函数 在
在 内有极小值,则实数
内有极小值,则实数 的取值范围为( )
的取值范围为( )
A. | B. | C. | D. |
函数y=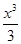 -x2+1(0<x<2)的图象上任意点处切线的倾斜角记为α,则α的最小值是( )
-x2+1(0<x<2)的图象上任意点处切线的倾斜角记为α,则α的最小值是( )
A.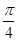 | B.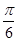 | C.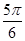 | D.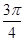 |
设f(x)=- x3+
x3+ x2+2ax,若f(x)在(
x2+2ax,若f(x)在( ,+∞)上存在单调递增区间,则实数a的取值范围为( )
,+∞)上存在单调递增区间,则实数a的取值范围为( )
A.a>- | B.a<- | C.a> | D.不存在 |