题目内容
4．已知sinα-cosα=$\frac{1}{5}$，0≤α≤π，则sin2α=$\frac{24}{25}$，sin（2α-$\frac{π}{4}$）=$\frac{31\sqrt{2}}{50}$．分析 由sinα-cosα=$\frac{1}{5}$，两边平方，再利用同角三角函数基本关系式、倍角公式，两角和与差的正弦函数公式即可得出．
解答 解：∵sinα-cosα=$\frac{1}{5}$，0≤2α≤2π，
∴两边平方可得：1-sin2α=$\frac{1}{25}$，可得：sin2α=$\frac{24}{25}$．
∵sinα-cosα=$\frac{1}{5}$＞0，0≤α≤π，
∴sinα＞cosα，$\frac{π}{4}$＜α≤π，可得：$\frac{π}{2}$＜2α≤2π，
又∵sin2α=$\frac{24}{25}$＞0，可得：0＜2α＜π，从而可得：$\frac{π}{2}$＜2α＜π，
∴cos2α=-$\sqrt{1-si{n}^{2}2α}$=-$\frac{7}{25}$，
∴sin（2α-$\frac{π}{4}$）=$\frac{\sqrt{2}}{2}$（sin2α-cos2α）=$\frac{\sqrt{2}}{2}$×（$\frac{24}{25}$+$\frac{7}{25}$）=$\frac{31\sqrt{2}}{50}$．
故答案为：$\frac{24}{25}$，$\frac{31\sqrt{2}}{50}$．
点评 本题考查了同角三角函数基本关系式、倍角公式，两角和与差的正弦函数公式的应用，属于基础题．
练习册系列答案
相关题目
14．已知函数f（x）=ex的图象与函数g（x）=|ln（-x）|的图象有两个交点A（x1，y1），B（x2，y2），则（ ）
| A． | $\frac{1}{10}$＜x1x2＜$\frac{1}{e}$ | B． | $\frac{1}{e}$＜x1x2＜1 | C． | 1＜x1x2＜e | D． | x1x2＞e |
15．
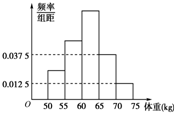为了了解某县今年高考准备报考体育专业的学生的体重情况，将所得的学生体重数据分组整理后，画出了频率分布直方图（如图），已知图中从左到右的前3小组的频率a，b，c恰成等差数列，若抽取的学生人数是48，则第2小组的频数为（ ）
为了了解某县今年高考准备报考体育专业的学生的体重情况，将所得的学生体重数据分组整理后，画出了频率分布直方图（如图），已知图中从左到右的前3小组的频率a，b，c恰成等差数列，若抽取的学生人数是48，则第2小组的频数为（ ）| A． | 6 | B． | 12 | C． | 18 | D． | 24 |
9．已知双曲线C1：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点F也是抛物线C2：y2=2px（p＞0）的焦点，C1与C2的一个交点为P，若PF⊥x轴，则双曲线C1的离心率为（ ）
| A． | $\sqrt{2}$+1 | B． | 2$\sqrt{2}$ | C． | 2$\sqrt{2}$-1 | D． | $\sqrt{3}$+1 |
16．二次函数y=kx2（x＞0）的图象在点（an，an2）处的切线与x轴交点的横坐标为an+1，n为正整数，a1=$\frac{1}{3}$，若数列{an}的前n项和为Sn，则S5=（ ）
| A． | $\frac{3}{2}[{1-{{（{\frac{1}{3}}）}^5}}]$ | B． | $\frac{1}{3}[{1-{{（{\frac{1}{3}}）}^5}}]$ | C． | $\frac{2}{3}[{1-{{（{\frac{1}{2}}）}^5}}]$ | D． | $\frac{3}{2}[{1-{{（{\frac{1}{2}}）}^5}}]$ |