题目内容
【题目】在我国古代著名的数学专著《九章算术》里有﹣段叙述：今有良马与驽马发长安至齐，齐去长安一千一百二十五里，良马初日行一百零三里，日增十三里：驽马初日行九十七里，日减半里，良马先至齐，复还迎驽马，二马相逢， 问：需日相逢．
【答案】9
【解析】解：由题意知，良马每日行的距离成等差数列， 记为{an}，其中a1=103，d=13；
驽马每日行的距离成等差数列，
记为{bn}，其中b1=97，d=﹣0.5；
设第m天相逢，则a1+a2+…+am+b1+b2+…+bm
=103m+ 
+97m+ 
=2×1125，
解得：m=9．
故答案为：9．
良马每日行的距离成等差数列，记为{an}，其中a1=103，d=13；驽马每日行的距离成等差数列，记为{bn}，其中b1=97，d=﹣0.5．求和即可得到答案．
练习册系列答案
智慧课堂密卷100分单元过关检测系列答案
单元期中期末卷系列答案
相关题目
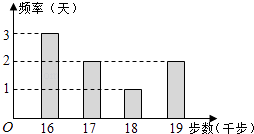
【题目】小王为了锻炼身体，每天坚持“健步走”，并用计步器进行统计．小王最近8天“健步走”步数的频数分布直方图（图1）及相应的消耗能量数据表（表1）如下：
健步走步数（前步） | 16 | 17 | 18 | 19 |
消耗能量（卡路里） | 400 | 440 | 480 | 520 |
（Ⅰ）求小王这8天“健步走”步数的平均数；
（Ⅱ）从步数为17千步，18千步，19千步的几天中任选2天，求小王这2天通过“健步走”消耗的能量和不小于1000卡路里的概率．
