题目内容
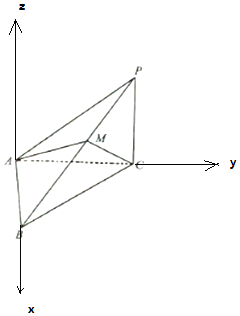
【题目】如图,在三棱锥P﹣ABC中,PC⊥平面ABC,∠ACB=45°,BC=2 ![]() ,AB=2.
,AB=2. 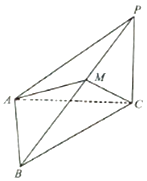
(1)求AC的长;
(2)若PC= ![]() ,点M在侧棱PB上,且
,点M在侧棱PB上,且 ![]() =
= ![]() ,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
,当λ为何值时,二面角B﹣AC﹣M的大小为30°.
【答案】
(1)解:在△ABC中,
由余弦定理得AB2=BC2+AC2﹣2BC×AC×cos∠ACB,
得4=8+AC2+﹣4AC,解得AC=2
(2)解:∵PC⊥平面ABC,PA⊥AB,∴AB⊥AC,
以A为原点,AB为x轴,AC为y轴,过A作平面ABC的垂线为z轴,建立空间直角坐标系,
B(2,0,0),C(0,2,0),P(0,2, ![]() ),
),
∵点M在侧棱PB上,且 ![]() =
= ![]() ,
,
∴M( ![]() ,
, ![]() ,
, ![]() ),
),
设平面ACM的一个法向量为 ![]() =(x,y,z),
=(x,y,z),
则 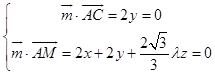 ,取z=1,得
,取z=1,得 ![]() =(﹣
=(﹣ ![]() ,0,1),
,0,1),
平面ABC的一个法向量 ![]() =(0,0,1),
=(0,0,1),
∵二面角B﹣AC﹣M的大小为30°,
∴cos30°= ![]() =
= 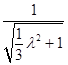 =
= ![]() ,
,
解得λ=1或λ=﹣1(舍),
∴当λ=1时,二面角B﹣AC﹣M的大小为30°.
【解析】(1)由已知条件利用余弦定理,利能求出AC.(2)以A为原点,AB为x轴,AC为y轴,过A作平面ABC的垂线为z轴,建立空间直角坐标系,求出平面ACM的一个法向量和平面ABC的一个法向量,利用向量法能求出当λ=1时,二面角B﹣AC﹣M的大小为30°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目