Question

【题目】已知△ABC的三个内角A，B，C所对的边分别为a，b，c，且asinAsinB+bcos2A= a．
（1）求 ；
（2）若c2=a2+ b2 ， 求角C．

Answer 1

【答案】
（1）解：△ABC中，asinAsinB+bcos2A= a，

由正弦定理化简得：sin2AsinB+sinBcos2A= sinA，

即sinB（sin2A+cos2A）= sinA，

∴sinB= sinA，

再由正弦定理得：b= a，

则 =

（2）解：由（1）可得b= a，

c2=a2+ b2=a2+ × a2= a2，

由余弦定理可得：

cosC= = = ，

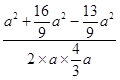由C为三角形内角，可得∠C=

【解析】（Ⅰ）利用正弦定理化简已知的等式，整理后利用同角三角函数间的基本关系化简，得到sinB=2sinA， 再利用正弦定理化简，即可得到所求式子的值；（2）由余弦定理可求cosC的值，结合C的范围即可得解．
【考点精析】根据题目的已知条件，利用余弦定理的定义的相关知识可以得到问题的答案，需要掌握余弦定理:;;．