题目内容
13.已知等差数列{an}中,a3=6,a6=3,则a9=0.分析 在等差数列{an}中,设出公差为d,根据a3=6,a6=3,求出公差和首项,然后求出等差数列的通项公式,从而求解.
解答 解:在等差数列{an}中,a3=6,a6=3,
a1+2d=6①,a1+5d=3②,
联立①②可得,3d=-3,d=-1;
a1=8,∴an=a1+(n-1)d=8+(n-1)×(-1)=9-n;
∴a9=0,
故答案为:0.
点评 本题主要考查等差数列的通项公式及其应用,考查解方程的运算求解能力,属于基础题.

练习册系列答案
相关题目
3.在数列{an}中,若存在非零整数T,使得am+T=am对于任意的正整数m均成立,那么称数列{an}为周期数列,其中T叫做数列{an}的周期.若数列{xn}满足xn+1=|xn-xn-1|(n≥2,n∈N),如x1=1,x2=a(a∈R,a≠0),当数列{xn}的周期最小时,该数列的前2015项的和是( )
| A. | 671 | B. | 672 | C. | 1342 | D. | 1344 |
8.双曲线C的中心在原点,焦点在y轴上,离心率为$\sqrt{2}$,双曲线C与抛物线y2=4x的准线交于A,B两点,|AB|=4,则双曲线C的实轴长为( )
| A. | 2 | B. | $\sqrt{3}$ | C. | 4 | D. | $2\sqrt{3}$ |
5.已知全集U=R,M={x|x2<2x},则∁UM=( )
| A. | {x|X≥2} | B. | {x|x>2} | C. | {x|x≤0或x≥2} | D. | {x|0<x<2} |
2.若a>0且a≠1,函数y=ax-3+1的反函数图象一定过点A,则A的坐标是( )
| A. | (1,0) | B. | (0,1) | C. | (2,3) | D. | (3,2) |
7.设i是虚数单位,若z=cosθ+isinθ且对应的点位于复平面的第二象限,则θ位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
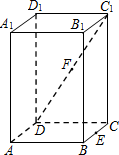 如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题:
如图,在正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1中,E是BC的中点,F是C1D的中点,P是棱CC1所在直线上的动点.则下列四个命题: 在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,AC⊥FB.
在如图所示的几何体中,四边形CDEF为正方形,四边形ABCD为等腰梯形,AB∥CD,AC=$\sqrt{3}$,AB=2BC=2,AC⊥FB.