题目内容
3.在数列{an}中,若存在非零整数T,使得am+T=am对于任意的正整数m均成立,那么称数列{an}为周期数列,其中T叫做数列{an}的周期.若数列{xn}满足xn+1=|xn-xn-1|(n≥2,n∈N),如x1=1,x2=a(a∈R,a≠0),当数列{xn}的周期最小时,该数列的前2015项的和是( )| A. | 671 | B. | 672 | C. | 1342 | D. | 1344 |
分析 ①若其最小周期为1,则该数列是常数列,即每一项都等于1,此时a=1,而该数列的项分别为1,1,0,1,1,0,1,1,0,…,即此时该数列是以3为周期的数列,矛盾,舍去.②若其最小周期为2,同理得出矛盾,舍去.综上所述,当数列{xn}的周期最小时,其最小周期是3,a=1,即可得出.
解答 解:①若其最小周期为1,则该数列是常数列,即每一项都等于1,此时a=1,
而该数列的项分别为1,1,0,1,1,0,1,1,0,…,即此时该数列是以3为周期的数列,矛盾,舍去.
②若其最小周期为2,则有a3=a1,即|a-1|=1,a-1=1或-1,a=2或a=0,又a≠0,故a=2,
此时该数列的项依次为1,2,1,1,0,…,由此可见,此时它并不是以2为周期的数列,舍去.
③综上所述,当数列{xn}的周期最小时,其最小周期是3,a=1,又2 015=3×671+2,
故此时该数列的前2 015项和是671×(1+1+0)+(1+1)=1344.
故选:D.
点评 本题考查了数列的周期性、分类讨论思想方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
13.P是△AOB所在平面上一点,且在AB的垂直平分线上,若|OA|=3,|OB|=2,则$\overrightarrow{OP}$•$\overrightarrow{AB}$=( )
| A. | $\frac{3}{2}$ | B. | -3 | C. | -$\frac{5}{2}$ | D. | 5 |
14.已知函数f(x)=|2x-1|,f(a)>f(b)>f(c),则以下情况不可能发生的是( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
11.五个人坐成一排,甲要和乙坐在一起,乙不和丙坐在一起,则不同排法数为( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
18.过抛物线x2=4y的焦点F作倾斜角为α的直线交抛物线于P、Q两点,过点P作抛物线的切线l交y轴于点T,过点P作切线l的垂线交y轴于点N,则△PNF为( )
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
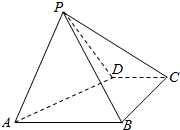 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD 是以AD为底的等腰三角形.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD 是以AD为底的等腰三角形.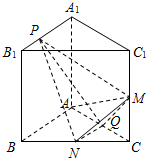 如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M,N,Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动.
如图,已知直三棱柱ABC-A1B1C1中,AA1=AB=AC,AB⊥AC,M,N,Q分别是CC1,BC,AC的中点,点P在线段A1B1上运动.