题目内容
【题目】如图，F1，F2分别是椭圆C：
的左、右焦点，A是椭圆C的顶点，B是直线AF2与椭圆C的另一个交点，∠F1AF2＝60°.
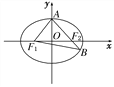
(1)求椭圆C的离心率；
(2)已知△AF1B的面积为40
，求a，b的值．
【答案】（1）
；（2）
.
【解析】(1)由题意可知，△AF1F2为等边三角形，a＝2c，所以e＝
.
(2)方法一：a2＝4c2，b2＝3c2，直线AB的方程为y＝－
(x－c)，
将其代入椭圆方程3x2＋4y2＝12c2，得B
，
所以|AB|＝
..
由S△AF1B＝|AF1|·|AB|·sin∠F1AB＝a·
c·
＝
a2＝40，
解得a＝10，b＝5.
方法二：设|AB|＝t.因为|AF2|＝a，所以|BF2|＝t－a，
由椭圆定义|BF1|＋|BF2|＝2a可知，|BF1|＝3a－t，
再由余弦定理(3a－t)2＝a2＋t2－2atcos 60°可得，t＝
a，
由S△AF1B＝aa＝a2＝40知，a＝10，b＝5.
黄冈创优卷系列答案
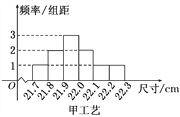
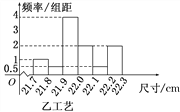
【题目】某工厂用甲、乙两种不同工艺生产一大批同一种零件，零件尺寸均在[21.7，22.3](单位：cm)之间，把零件尺寸在[21.9,22.1)的记为一等品，尺寸在[21.8,21.9)∪[22.1,22.2)的记为二等品，尺寸在[21.7，21.8)∪[22.2，22.3]的记为三等品，现从甲、乙工艺生产的零件中各随机抽取100件产品，所得零件尺寸的频率分布直方图如图所示．
P(K2≥k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
附：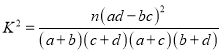 
(1)根据上述数据完成下列2×2列联表，根据此数据，你认为选择不同的工艺与生产出一等品是否有关？
甲工艺 | 乙工艺 | 总计 | |
一等品 | |||
非一等品 | |||
总计 |
(2)以上述各种产品的频率作为各种产品发生的概率，若一等品、二等品、三等品的单件利润分别为30元、20元、15元，你认为以后该工厂应该选择哪种工艺生产该种零件？请说明理由．
