��Ŀ����
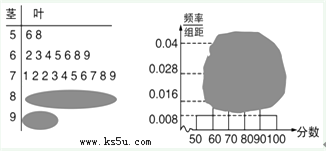
����Ŀ��ij�����üס������ֲ�ͬ��������һ����ͬһ�����������ߴ����[21.7��22.3](��λ��cm)֮�䣬������ߴ���[21.9,22.1)�ļ�Ϊһ��Ʒ���ߴ���[21.8,21.9)��[22.1,22.2)�ļ�Ϊ����Ʒ���ߴ���[21.7��21.8)��[22.2��22.3]�ļ�Ϊ����Ʒ���ִӼס��ҹ�������������и������ȡ100����Ʒ����������ߴ��Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
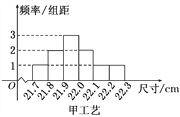
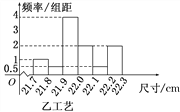
P(K2��k0) | 0.10 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
���� 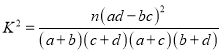
(1)�������������������2��2�����������ݴ����ݣ�����Ϊѡ��ͬ�Ĺ�����������һ��Ʒ�Ƿ��йأ�
���� | �ҹ��� | �ܼ� | |
һ��Ʒ | |||
��һ��Ʒ | |||
�ܼ� |
(2)���������ֲ�Ʒ��Ƶ����Ϊ���ֲ�Ʒ�����ĸ��ʣ���һ��Ʒ������Ʒ������Ʒ�ĵ�������ֱ�Ϊ30Ԫ��20Ԫ��15Ԫ������Ϊ�Ժ�ù���Ӧ��ѡ�����ֹ������������������˵�����ɣ�
���𰸡�(1)�������������� û��������Ϊѡ��ͬ�Ĺ�����������һ��Ʒ�йأ�(2) ѡ�����
�������������������1���������������������ݣ�д����������ע�����ֱȽ϶࣬��Ҫд��λ�ã������������������������ݴ�����۲�ֵ�Ĺ�ʽ������۲�ֵ���ѹ۲�ֵͬ�ٽ�ֵ���бȽϣ��õ����ۣ���2������������ճ�ȡ��100����Ʒ�У�һ��Ʒ��50��������Ʒ��30��������Ʒ��20�����������������������ȡ��100����Ʒ�ĵ��������ƽ������
���������
(1)2��2���������£�
���� | �ҹ��� | �ܼ� | |
һ��Ʒ | 50 | 60 | 110 |
��һ��Ʒ | 50 | 40 | 90 |
�ܼ� | 100 | 100 | 200 |
K2��![]() ��2.02<2.706������û��������Ϊѡ��ͬ�Ĺ�����������һ��Ʒ�йأ�
��2.02<2.706������û��������Ϊѡ��ͬ�Ĺ�����������һ��Ʒ�йأ�
(2)����֪���ü�������������Ʒ������X�ķֲ���Ϊ
X | 30 | 20 | 15 |
P | 0.5 | 0.3 | 0.2 |
X�ľ�ֵΪE(X)��30��0.5��20��0.3��15��0.2��24��
X�ķ���ΪD(X)��(30��24)2��0.5��(20��24)2��0.3��(15��24)2��0.2��39.
�ҹ�������������Ʒ������Y�ķֲ���Ϊ
Y | 30 | 20 | 15 |
P | 0.6 | 0.1 | 0.3 |
Y�ľ�ֵΪE(Y)��30��0.6��20��0.1��15��0.3��24.5��Y�ķ���ΪD(Y)��(30��24.5)2��0.6��(20��24.5)2��0.1��(15��24.5)2��0.3��47.25.
������������Կ���D(X)<D(Y)�������ղ���С����ȻE(X)<E(Y)�������������Ժ�ѡ����գ�

 ��״Ԫ���źþ�ϵ�д�
��״Ԫ���źþ�ϵ�д�