题目内容
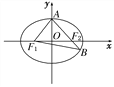
【题目】已知点![]() 是椭圆E:
是椭圆E:![]() (a>b>0)上一点,离心率为
(a>b>0)上一点,离心率为![]() .
.
(1)求椭圆E的方程;
(2)设不过原点O的直线l与该椭圆E交于P,Q两点,满足直线OP,PQ,OQ的斜率依次成等比数列,求△OPQ面积的取值范围.
【答案】(1)![]() (2)(0,
(2)(0,![]() ).
).
【解析】试题分析:(1)根据离心率得a,b,c三者关系,再代入点![]() 可得a2=4,b2=3.(2)因为直线OP,PQ,OQ的斜率依次成等比数列,可得
可得a2=4,b2=3.(2)因为直线OP,PQ,OQ的斜率依次成等比数列,可得![]() ,再直线l的方程为y=kx+m(m≠0),联立直线方程与椭圆方程,利用韦达定理代入关系式得
,再直线l的方程为y=kx+m(m≠0),联立直线方程与椭圆方程,利用韦达定理代入关系式得![]() ,根据点到直线距离公式得高,根据弦长公式得底边边长,结合三角形面积公式得关于m函数关系式,最后利用基本不等式求最值,得取值范围
,根据点到直线距离公式得高,根据弦长公式得底边边长,结合三角形面积公式得关于m函数关系式,最后利用基本不等式求最值,得取值范围
试题解析:解:(1)由题意知,![]() =
=![]() ,
,
所以![]() =
=![]() ,a2=
,a2=![]() b2.
b2.
又![]() +
+![]() =1,解得a2=4,b2=3.
=1,解得a2=4,b2=3.
因此椭圆E的方程为![]()
(2)由题意可知,直线l的斜率存在且不为0,
故可设直线l的方程为y=kx+m(m≠0),
P(x1,y1),Q(x2,y2),
由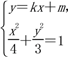 消去y得,
消去y得,
(3+4k2)x2+8kmx+4(m2-3)=0.
由题意知Δ=64k2m2-16(3+4k2)(m2-3)
=16(12k2-3m2+9)>0,
即4k2-m2+3>0.
又x1+x2=-![]() ,x1x2=
,x1x2=![]()
所以y1y2=(kx1+m)(kx2+m)
=k2x1x2+km(x1+x2)+m2=![]() .
.
因为直线OP,PQ,OQ的斜率依次成等比数列,
所以![]() ·
·![]() =
=![]() =k2,
=k2,
即(4k2-3)m2=0,
∵m≠0,∴k2=![]() .
.
由于直线OP,OQ的斜率存在,且Δ>0,
得0<m2<6,且m2≠3.
设d为点O到直线l的距离,
则S△OPQ=![]() d|PQ|
d|PQ|
=![]() ×
×![]()
![]() |x1-x2|
|x1-x2|
=![]() |m|
|m|![]()
又因为m2≠3,
所以S△OPQ=![]()
![]() <
<![]() ×
×![]() =
=![]() .
.
所以△OPQ面积的取值范围为(0,![]() ).
).

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目