题目内容
已知抛物线y2=-8mx(m>0),是否存在过抛物线的焦点F的弦PQ,使△POQ的面积最大或最小?若存在,求出PQ所在直线的倾斜角;若不存在,请说明理由.
1、S△POQ=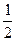
·8m·2m=8m2.
2、S△POQ有最小值,且最小值为8m2,此时倾斜角为90°,但S△POQ无最大值.
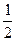·8m·2m=8m2.2、S△POQ有最小值,且最小值为8m2,此时倾斜角为90°,但S△POQ无最大值.
(1)当PQ垂直于x轴时,S△POQ=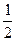·8m·2m=8m2.
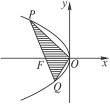
(2)当PQ不与x轴垂直时,设PQ:y=k(x+2m)(k≠0),即x=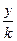
-2m.
代入抛物线方程得ky2+8my-16km2=0.
故可求得|y1-y2|=8m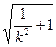
.
∴S△POQ=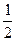|y1-y2|·|OF|=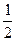|y1-y2|·2m=4m
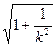·2m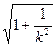=8m2·>8m2.
∴S△POQ有最小值,且最小值为8m2,此时倾斜角为90°,但S△POQ无最大值.
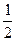·8m·2m=8m2.(2)当PQ不与x轴垂直时,设PQ:y=k(x+2m)(k≠0),即x=
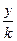-2m.代入抛物线方程得ky2+8my-16km2=0.
故可求得|y1-y2|=8m
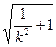.∴S△POQ=
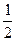|y1-y2|·|OF|=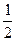|y1-y2|·2m=4m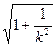·2m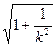=8m2·>8m2.∴S△POQ有最小值,且最小值为8m2,此时倾斜角为90°,但S△POQ无最大值.
练习册系列答案
阅读快车系列答案
相关题目
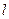应设计为多少？
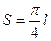h）？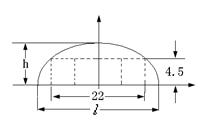
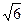,求抛物线的方程.
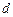万公里时，经过地球和慧得的直线与抛物线对称轴的夹角为
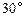，求此慧星运行时离地球的最近距离．