题目内容
顶点在原点,焦点在x轴上的抛物线被直线y=x-2截得的线段长为4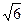
,求抛物线的方程.
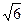,求抛物线的方程.y2=-12x或y2=4x.
设所求抛物线方程为y2=ax(a≠0).
它与直线y=x-2交于A(x1,y1)、B(x2,y2)两点.
由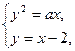
得x2-(4+a)x+4=0.
∴
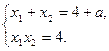
∴|AB|=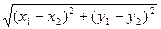
=
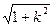|x1-x2|
=
.
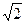
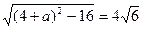∴a2+8a-48=0.
∴a=-12或a=4,此时Δ>0恒成立.
故所求抛物线方程为y2=-12x或y2=4x.
它与直线y=x-2交于A(x1,y1)、B(x2,y2)两点.
由
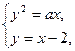得x2-(4+a)x+4=0.∴
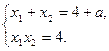
∴|AB|=
=
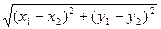
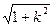|x1-x2|=
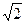
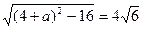.∴a2+8a-48=0.
∴a=-12或a=4,此时Δ>0恒成立.
故所求抛物线方程为y2=-12x或y2=4x.
练习册系列答案
相关题目
直线AB过抛物线x2=2py（p>0）的焦点F，并与其相交于A、B两点，Q是线段AB的中点，M是抛物线的准线与y轴的交点，O是坐标原点.
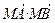的取值范围；
；
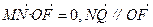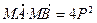，△ABN的面积的取值范围为［5
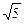，20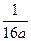
)
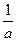x2(a≠0)的焦点坐标是__________.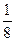
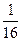
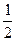时,方程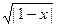
=kx的解的个数是( )
（
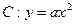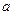为非零常数）的焦点为
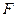，点
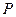为抛物线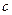
上一个动点，过点
．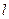