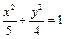题目内容
(本小题满分14分)已知椭圆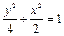 两焦点分别为
两焦点分别为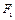 、
、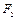 ,
,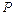 是椭圆在第一象限弧上的一点,并满足
是椭圆在第一象限弧上的一点,并满足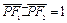 ,过点
,过点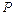 作倾斜角互补的两条直线
作倾斜角互补的两条直线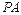 、
、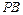 分别交椭圆于
分别交椭圆于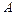 、
、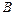 两点.
两点.
(1)求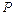 点坐标;
点坐标;
(2)证明:直线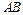 的斜率为定值,并求出该定值;
的斜率为定值,并求出该定值;
(3)求△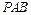 面积的最大值.
面积的最大值.
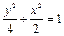 两焦点分别为
两焦点分别为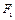 、
、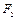 ,
,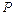 是椭圆在第一象限弧上的一点,并满足
是椭圆在第一象限弧上的一点,并满足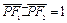 ,过点
,过点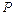 作倾斜角互补的两条直线
作倾斜角互补的两条直线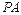 、
、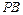 分别交椭圆于
分别交椭圆于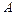 、
、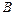 两点.
两点.(1)求
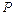 点坐标;
点坐标;(2)证明:直线
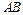 的斜率为定值,并求出该定值;
的斜率为定值,并求出该定值;(3)求△
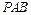 面积的最大值.
面积的最大值.(1)点P的坐标为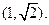
(2)直线AB斜率为定值,值为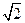 .
.
(3)△PAB面积的最大值为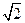 .
.
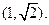
(2)直线AB斜率为定值,值为
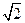 .
.(3)△PAB面积的最大值为
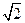 .
.解:(1)由题可得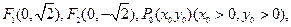
则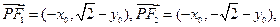
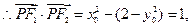 ①
①
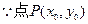 在曲线上,则
在曲线上,则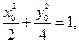 ②
②
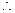 由①②得
由①②得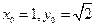 ,则点P的坐标为
,则点P的坐标为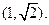 ………(4分)
………(4分)
(2)设直线PA斜率K,则直线PB斜率-K,设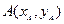 ,
,
则直线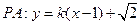 与椭圆方程联立得:
与椭圆方程联立得:
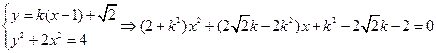
由韦达定理: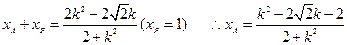
同理求得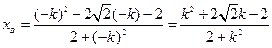
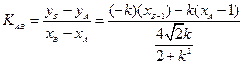
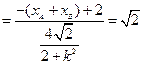
综上,直线AB斜率为定值,值为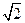 . …………(9分)
. …………(9分)
(3)设AB的直线方程: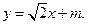
由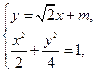 ,得
,得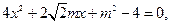
由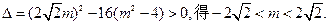
P到AB的距离为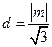 ,
,
则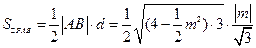
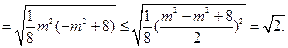
当且仅当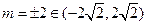 时取等号,
时取等号,
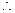 △PAB面积的最大值为
△PAB面积的最大值为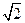 . …………(14分)
. …………(14分)
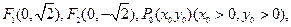
则
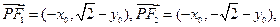
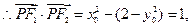 ①
①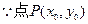 在曲线上,则
在曲线上,则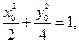 ②
②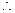 由①②得
由①②得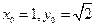 ,则点P的坐标为
,则点P的坐标为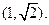 ………(4分)
………(4分)(2)设直线PA斜率K,则直线PB斜率-K,设
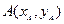 ,
,则直线
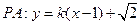 与椭圆方程联立得:
与椭圆方程联立得: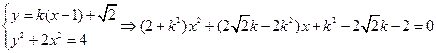
由韦达定理:
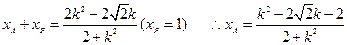
同理求得
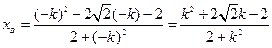
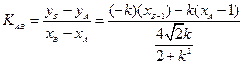
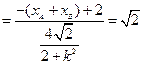
综上,直线AB斜率为定值,值为
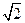 . …………(9分)
. …………(9分)(3)设AB的直线方程:
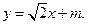
由
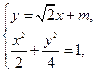 ,得
,得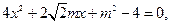
由
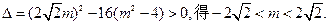
P到AB的距离为
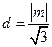 ,
,则
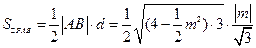
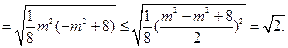
当且仅当
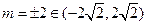 时取等号,
时取等号,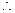 △PAB面积的最大值为
△PAB面积的最大值为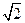 . …………(14分)
. …………(14分)
练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
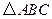 的顶点
的顶点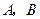 在椭圆
在椭圆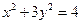 上,
上,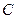 在直线
在直线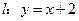 上,且
上,且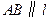 .
.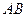 边通过坐标原点
边通过坐标原点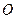 时,求
时,求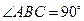 ,且斜边
,且斜边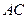 的长最大时,求
的长最大时,求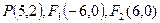
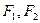 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;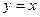 的对称点分别为
的对称点分别为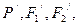 ,求以
,求以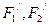 为焦点且过点
为焦点且过点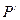 的双曲线的标准方程。
的双曲线的标准方程。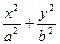 =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.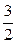 )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;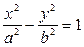 写出具有类似特性的性质,并加以证明.
写出具有类似特性的性质,并加以证明. +
+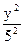 =1的焦点坐标为(0,4)和(0,—4).
=1的焦点坐标为(0,4)和(0,—4).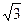 =0垂直的直线方程是2x + y-3=0.
=0垂直的直线方程是2x + y-3=0.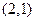 的距离与到定直线
的距离与到定直线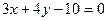 距离相等的点的轨迹是抛物线.
距离相等的点的轨迹是抛物线.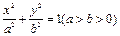 的左焦点
的左焦点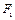 作
作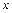 轴的垂线交椭圆于点
轴的垂线交椭圆于点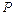 ,
,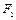 为右焦点,若
为右焦点,若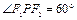 ,则椭圆的离心率为( )
,则椭圆的离心率为( )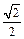
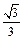
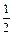
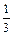
 已知
已知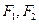 是椭圆
是椭圆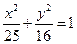 的两个焦点,P是椭圆上的一点,若
的两个焦点,P是椭圆上的一点,若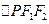 的内切圆半径为1,则点P到x轴的距离为( )
的内切圆半径为1,则点P到x轴的距离为( )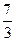

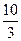
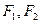 是椭圆
是椭圆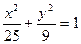 的两个焦点,过
的两个焦点,过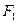 作直线与椭圆交于A,B两点,
作直线与椭圆交于A,B两点,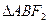 的周长为
的周长为 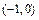 、B
、B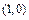 ,以AB为一腰作使∠DAB=
,以AB为一腰作使∠DAB=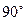 直角梯形ABCD,且
直角梯形ABCD,且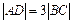 ,CD中点的纵坐标为1.若椭圆以A、B为焦点且经过点D,则此椭圆的方程为
,CD中点的纵坐标为1.若椭圆以A、B为焦点且经过点D,则此椭圆的方程为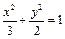 B.
B.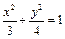 C.
C.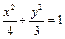 D.
D.