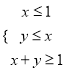题目内容
【题目】已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,∠B的平分线BN所在直线方程为x﹣2y﹣5=0.求:
(1)顶点B的坐标;
(2)直线BC的方程.
【答案】
(1)解:设B(x0,y0),由AB中点在2x﹣y﹣5=0上,可得2 ![]() ﹣
﹣ ![]() ﹣5=0
﹣5=0
即2x0﹣y0﹣1=0,联立x0﹣2y0﹣5=0解得B(﹣1,﹣3)
(2)解:设A点关于x﹣2y+5=0的对称点为A′(x′,y′),
则有 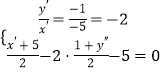
解得A′( ![]() ,
, ![]() )
)
∴BC边所在的直线方程为y+3= ![]() (x+1),即18x﹣31y﹣75=0
(x+1),即18x﹣31y﹣75=0
【解析】(1)设B(x0 , y0),由AB中点在2x﹣y﹣5=0上,在直线方程为x﹣2y+5=0,求出B的坐标;(2)求出A关于x﹣2y﹣5=0的对称点为A′(x′,y′)的坐标,即可求出BC边所在直线的方程.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目