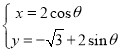题目内容
【题目】过抛物线![]() 的焦点
的焦点![]() 的直线交抛物线于
的直线交抛物线于![]() ,
, ![]() 两点,
两点, ![]() 为坐标原点,若
为坐标原点,若![]() ,则△
,则△![]() 的面积为( )
的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】【解法1】设∠AFx=θ(0<θ<π)及|BF|=m,∵|AF|=3,∴点A到准线l:x=-1的距离为3
∴2+3cosθ=3∴cosθ=![]() ,∵m=2+mcos(π-θ),∴
,∵m=2+mcos(π-θ),∴![]() ,
,
∴△AOB的面积为S=![]() ×
×![]() ×
×![]() ×sinθ=
×sinθ=![]() ×1×(3+
×1×(3+![]() )×
)×![]() =
=![]() .故选(C)
.故选(C)
【解法2】如图,设A![]()
![]() .易知抛物线y2=4x的焦点为F
.易知抛物线y2=4x的焦点为F![]() ,
,
准线为x=-1,故由抛物线的定义得![]() =x0-
=x0-![]() =3,解得x0=2,
=3,解得x0=2,
所以y0=-2![]() ,故A
,故A![]() .则直线AB斜率为k=
.则直线AB斜率为k=![]() =-2
=-2![]() ,
,
直线AB的方程为y=-2![]() x+2
x+2![]() ,联立
,联立![]()
消去y得2x2-5x+2=0,由x1x2=1,得A,B两点横坐标之积为1,所以点B的横坐标为![]() .
.
再由抛物线的定义得![]() =
=![]() -
-![]() =
=![]() ,
,![]() =
=![]() +
+![]() =3+
=3+![]() =
=![]() .
.
又因为点O到直线AB的距离为d=![]() ,所以S△AOB=
,所以S△AOB=![]() ×
×![]() ×
×![]() =
=![]() .故选(C)
.故选(C)

练习册系列答案
相关题目
【题目】某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数 | 1 | 1 | 1 | 2 | 2 | 1 | 2 |
用水量/吨 | 22 | 38 | 40 | 41 | 44 | 50 | 95 |
(Ⅰ)在这10天中,该公司用水量的平均数是多少?每天用水量的中位数是多少?
(Ⅱ)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?