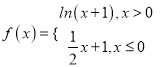Question

【题目】有以下命题：
①若f（x）=x3+（a﹣1）x2+3x+1没有极值点，则﹣2＜a＜4；
②集合M={1，2，zi}，i为虚数单位，N={3，4}，M∩N={4}，则复数z=﹣4i；
③若函数f（x）= ﹣m有两个零点，则m＜ ．
其中正确的是 ．

Answer 1

【答案】②
【解析】解：①若f（x）=x3+（a﹣1）x2+3x+1，
则f′（x）=3x2+2（a﹣1）x+3，
若f（x）没有极值点，则△≤0，
即4（a﹣1）2﹣36≤0，
即（a﹣1）2≤9，
得﹣3≤a﹣1≤3，则﹣2≤a≤4，故①错误，
②集合M={1，2，zi}，i为虚数单位，N={3，4}，M∩N={4}，
则zi=4，则z= =﹣4i；故②正确，
③若函数f（x）= ﹣m有两个零点，则f（x）= ﹣m=0，即 =m有两个根，
设g（x）= 则g′（x）= ，
由g′（x）＞0得1﹣lnx＞0得0＜x＜e，
g′（x）＜0得1﹣lnx＜0得x＞e，
即当x=e时，函数f（x）取得极大值g（e）= = ，
当x＞e时，g（x）= ＞0，
则若 =m有两个根，
则0＜m＜ ．故③错误，
所以答案是：②
【考点精析】根据题目的已知条件，利用命题的真假判断与应用的相关知识可以得到问题的答案，需要掌握两个命题互为逆否命题，它们有相同的真假性；两个命题为互逆命题或互否命题，它们的真假性没有关系．