题目内容
4.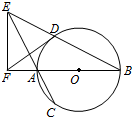 如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.
如图AB是⊙O的直径,弦BD,CA的延长线相交于点E,EF垂直BA的延长线于点F.求证:
(Ⅰ)A,D,E,F四点共圆;
(Ⅱ)AB2=BE•BD-AE•AC.
分析 (Ⅰ)证明∠ADB=90°,∠EFA=90°,即可证明A,D,E,F四点共圆;
(Ⅱ)由(Ⅰ)知,BD•BE=BA•BF,利用△ABC∽△AEF,可得AB2=BE•BD-AE•AC,即可证明结论.
解答  证明:(Ⅰ)连结AD,∵AB为圆的直径,∴∠ADB=90°,-----(3分)
证明:(Ⅰ)连结AD,∵AB为圆的直径,∴∠ADB=90°,-----(3分)
又EF⊥AB,∠EFA=90°,则A、D、E、F四点共圆,------------(6分)
(Ⅱ)由(Ⅰ)知,BD•BE=BA•BF.-----------------------(8分)
又△ABC∽△AEF,∴$\frac{AB}{AE}=\frac{AC}{AF}$,即AB•AF=AE•AC.--------(10分)
∴BE•BD-AE•AC=BA•BF-AB•AF=AB(BF-AF)=AB2.---------(12分)
点评 本题考查三角形相似的判断,考查四点共圆,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
19.观察下列散点图,则①正相关;②负相关;③不相关.它们的排列顺序与图形对应顺序正确的是( )


| A. | a,b,c | B. | b,a,c | C. | a,c,b | D. | c,a,b |
14.某机构对儿童记忆能力x和识图能力y进行统计分析,得到如下数据:
由表中数据,求得线性回归方程为$\stackrel{∧}{y}$=$\frac{4}{5}$$\stackrel{∧}{x}$+$\stackrel{∧}{a}$($\hat a=\overline y-\frac{4}{5}$$\overline x$),若某儿童记忆能力为12,则他识图能力为( )
| 记忆能力x | 4 | 6 | 8 | 10 |
| 识图能力y | 3 | 5 | 6 | 8 |
| A. | 9.2 | B. | 9.8 | C. | 9.5 | D. | 10 |
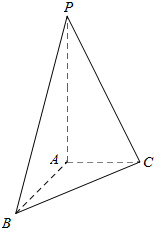 如图,在三棱锥P-ABC中,PA丄平面ABC,AC丄AB,PA=AB=2,AC=1.
如图,在三棱锥P-ABC中,PA丄平面ABC,AC丄AB,PA=AB=2,AC=1. 如图,圆O的半径为2,P是圆O的直径AB延长线上的一点,BP=1,割线PCD交圆O于C、D两点,过P作FP⊥AP,交直线AC于点E,交直线AD于点F.
如图,圆O的半径为2,P是圆O的直径AB延长线上的一点,BP=1,割线PCD交圆O于C、D两点,过P作FP⊥AP,交直线AC于点E,交直线AD于点F.