题目内容
8．
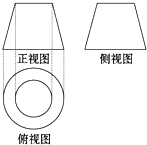如图是一个几何体的三视图，其中正视图和侧视图都是一个两底长分别为2和4，腰长为4的等腰梯形，则该几何体的侧面积是（ ）| A． | 6π | B． | 12π | C． | 18π | D． | 24π |
分析 该几何体的直观图是圆台，上底面是一个直径为2的圆，下底面是一个直径为4的圆，母线长是4，把直径变化为半径代入圆台的侧面积公式，求出结果．
解答 解：由三视图可知，正视图和侧视图都是一个两底长分别为2和4，
腰长为4的等腰梯形，该几何体的直观图是圆台，
上底面是一个直径为2的圆，下底面是一个直径为4的圆，母线长是4，
∴其圆台的侧面积是：π（1+2）×4=12π
故选：B．
点评 本题考查由三视图求几何体的侧面积，考查有三视图还原几何体，考查圆台的侧面积，对于圆台的表面积和侧面积这两个公式都要记清楚，会应用．
练习册系列答案
相关题目
19．观察下列散点图，则①正相关；②负相关；③不相关．它们的排列顺序与图形对应顺序正确的是（ ）
| A． | a，b，c | B． | b，a，c | C． | a，c，b | D． | c，a，b |
如图，圆O的半径为2，P是圆O的直径AB延长线上的一点，BP=1，割线PCD交圆O于C、D两点，过P作FP⊥AP，交直线AC于点E，交直线AD于点F．
20．为了得到函数y=sin（2x-$\frac{π}{4}$）的图象，只要将函数y=sin（x-$\frac{π}{4}$）上所有的点（ ）
| A． | 横坐标伸长到原来的2倍，纵坐标不变 | |
| B． | 横坐标缩短到原来的$\frac{1}{2}$倍，纵坐标不变 | |
| C． | 纵坐标伸长到原来的2倍，横坐标不变 | |
| D． | 纵坐标缩短到原来的$\frac{1}{2}$倍，横坐标不变 |
17．设点F为双曲线C：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的右焦点，直线l过原点且与双曲线C相交于A，B两点，若双曲线C的右顶点M恰为△ABF的重心，则双曲线C的离心率为（ ）
| A． | $\frac{4}{3}$ | B． | $\frac{3}{2}$ | C． | 2 | D． | 3 |