题目内容
【题目】下列四个命题中,真命题的个数是 ( )
①命题:“已知![]() ,“
,“![]() ”是“
”是“![]() ”的充分不必要条件”;
”的充分不必要条件”;
②命题:“p且q为真”是“p或q为真”的必要不充分条件;
③命题:已知幂函数![]() 的图象经过点(2,
的图象经过点(2,![]() ),则f(4)的值等于
),则f(4)的值等于![]() ;
;
④命题:若![]() ,则
,则![]() .
.
A. 1B. 2C. 3D. 4
【答案】C
【解析】
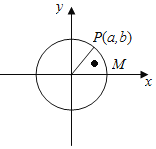
命题①单位圆x2+y2=1上或圆外任取一点P(a,b),满足“a2+b2≥1”,根据三角形两边之和大于第三边,一定有“|a|+|b|≥1”,在单位圆内任取一点M(a,b),满足“|a|+|b|≥1”,但不满足“a2+b2≥1”,从而判断命题的真假性;
命题②先由“p且q为真”推出p、q的真假,然后判断“p或q”的真假,反之再加以判断;
命题③直接把点的坐标代入幂函数求出α,然后把x=4代入求值即可;
命题④构造函数f(x)=x﹣1+lnx,其中x>0,利用导数判断函数的单调性,从而判断命题的真假性;
命题①如图在单位圆x2+y2=1上或圆外任取一点P(a,b),满足“a2+b2≥1”,根据三角形两边之和大于第三边,一定有“|a|+|b|≥1”,在单位圆内任取一点M(a,b),满足“|a|+|b|≥1”,但不满足,“a2+b2≥1”,故a2+b2≥1是“|a|+|b|≥1”的充分不必要条件,故命题①正确;
命题②“p且q为真”,则命题p、q均为真,所以“p或q为真”.反之“p或q为真”,则p、q都为真或p、q一真一假,所以不一定有“p且q为真”.所以命题“p且q为真”是“p或q为真”的充分不必要条件,故命题②不正确;
命题③由幂函数f(x)=xα的图象经过点(2,![]() ),所以2α=
),所以2α=![]() ,所以α=﹣
,所以α=﹣![]() ,所以幂函数为f(x)=
,所以幂函数为f(x)=![]() ,所以f(4)=
,所以f(4)=![]() ,所以命题③正确;
,所以命题③正确;
命题④若x+lnx>1,则x﹣1+lnx>0,设f(x)=x﹣1+lnx,其中x>0,
∴![]() >0恒成立,∴f(x)在(0,+∞)上单调递增,且f(1)=0,
>0恒成立,∴f(x)在(0,+∞)上单调递增,且f(1)=0,
∴f(x)>0时x>1,即x+lnx>1时x>1,所以命题④正确.
故选:C

【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店,为合理安排各地区加盟店的个数,先在其中5个地区试点,得到试点地区加盟店个数分别为1,2,3,4,5时,单店日平均营业额![]() (万元)的数据如下:
(万元)的数据如下:
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
(1)求单店日平均营业额![]() (万元)与所在地区加盟店个数
(万元)与所在地区加盟店个数![]() (个)的线性回归方程;
(个)的线性回归方程;
(2)根据试点调研结果,为保证规模和效益,在其他5个地区,该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元,求一个地区开设加盟店个数![]() 的所有可能取值;
的所有可能取值;
(3)小赵与小王都准备加入该公司的加盟店,根据公司规定,他们只能分别从其他五个地区(加盟店都不少于2个)中随机选一个地区加入,求他们选取的地区相同的概率.
(参考数据及公式:![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,其中
,其中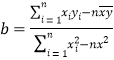 ,
,![]() .)
.)