题目内容
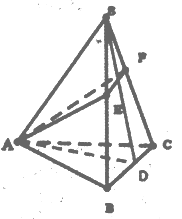
【题目】如图所示,已知正三棱锥![]() ,
,![]() 为
为![]() 中点,过点
中点,过点![]() 作截面
作截面![]() 交
交![]() ,
,![]() 分别于点
分别于点![]() ,
,![]() ,且
,且![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)在正三棱锥S﹣ABC中,由D为BC中点,可得BC⊥AD,且BC⊥SD,再由线面垂直的判定可得BC⊥平面SAD,由E,F分别为SB,SC的中点,可得EF∥BC,
则EF⊥平面SAD;
(2)在正三角形ABC中,由AB=2,求得AD,在等腰三角形SBC中,由已知求得SD,进一步求出正三棱锥的高,然后利用等积法求三棱锥S﹣AEF的体积.
详解:(1)证明:∵![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
又∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
∴![]() 平面
平面![]() .
.
(2)解:在![]() 中,
中,![]() ,
,![]() ,故
,故![]() (
(![]() 为底面中心),
为底面中心),
又由![]() .
.

练习册系列答案
相关题目

