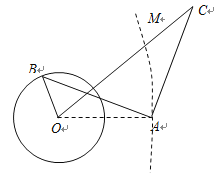
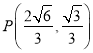题目内容
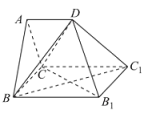
【题目】如图,多面体![]() 是正三棱柱(底面是正三角形的直棱柱)
是正三棱柱(底面是正三角形的直棱柱)![]() 沿平面
沿平面![]() 切除一部分所得,其中平面
切除一部分所得,其中平面![]() 为原正三棱柱的底面,
为原正三棱柱的底面,![]() ,点D为
,点D为![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的平面角的余弦值.
的平面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)设![]() 与
与![]() 交于点E,连接
交于点E,连接![]() 、
、![]() ,由题意可得四边形
,由题意可得四边形![]() 是正方形,且
是正方形,且![]() ,再由点D为
,再由点D为![]() 的中点,
的中点,![]() 平行且等于
平行且等于![]() ,求得CD,同理求得
,求得CD,同理求得![]() ,得
,得![]() ,可得
,可得![]() ,由线面垂直的判定可得;
,由线面垂直的判定可得;
(2)取BC的中点O,连接AO,可得AO⊥BC,由正棱柱的性质可得AO⊥平面![]() ,以O为坐标原点,向量
,以O为坐标原点,向量![]() 、
、![]() 、
、![]() 分别为x、y,z轴建立空间直角坐标系,分别求出平面CBD与平面
分别为x、y,z轴建立空间直角坐标系,分别求出平面CBD与平面![]() 的一个法向量,由两法向量所成角的余弦值可得二面角
的一个法向量,由两法向量所成角的余弦值可得二面角![]() 的平面角的余弦值.
的平面角的余弦值.
(1)设![]() 与
与![]() 交于点E,连接
交于点E,连接![]() 、
、![]() .
.
∵多面体![]() 是正三棱柱沿平面
是正三棱柱沿平面![]() 切除部分所得,
切除部分所得,![]() ,
,
∴四边形![]() 是正方形,且
是正方形,且![]() .
.
∵点D为![]() 的中点,
的中点,![]() 平行且等于
平行且等于![]() ,
,
∴![]() .
.
同理![]() ,
,
∴![]() .
.
∵E为![]() 的中点,
的中点,
∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ;
;
(2)取![]() 的中点O,连接
的中点O,连接![]() .
.
∵![]() 为正三角形,
为正三角形,![]() .
.
由正棱柱的性质可得,平面![]() 平面
平面![]() ,
,
且平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
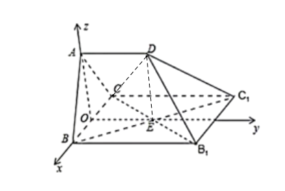
以点O为原点,向量![]() 、
、![]() 、
、![]() 分别为x、y,z轴正方向建立如图所示空间直角坐标系
分别为x、y,z轴正方向建立如图所示空间直角坐标系![]() .
.
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则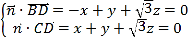 ,
,
令![]() ,得
,得![]() ,
,![]() ,即
,即![]() .
.
由(1)可知,平面![]() 的一个法向量为
的一个法向量为![]() .
.
 ,
,
又∵二面角![]() 的平面角为锐角,
的平面角为锐角,
∴二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某人某天的工作是驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() ,三地之间各路段行驶时间及拥堵概率如下表
,三地之间各路段行驶时间及拥堵概率如下表
路段 | 正常行驶所用时间(小时) | 上午拥堵概率 | 下午拥堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到拥堵,则在该路段行驶时间需要延长1小时.
现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事然后到达
地办事然后到达![]() 地,下午从
地,下午从![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]()
![]() 地出发到达
地出发到达![]() 地,办完事后返回
地,办完事后返回![]() 地.
地.
(1)若此人早上8点从![]() 地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率.
地的概率.
(2)甲乙两个方案中,哪个方案有利于办完事后更早返回![]() 地?请说明理由.
地?请说明理由.