题目内容
【题目】已知F1,F2为椭圆E:![]() 的左、右焦点,且|F1F2|=2
的左、右焦点,且|F1F2|=2![]() ,点
,点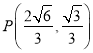 在E上.
在E上.
(1)求E的方程;
(2)直线l与以E的短轴为直径的圆相切,l与E交于A,B两点,O为坐标原点,试判断O与以AB为直径的圆的位置关系,并说明理由.
【答案】(1)![]() ;(2)O在以AB为直径的圆外,理由见解析
;(2)O在以AB为直径的圆外,理由见解析
【解析】
(1)根据![]() ,点
,点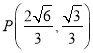 在
在![]() 上,结合
上,结合![]() ,即可得到;
,即可得到;
(2)分斜率不存在和斜率存在两种情况进行讨论.斜率不存在时,直接通过![]() 与半径比较即可;斜率存在时,设直线方程,联立方程组,利用韦达定理表示出
与半径比较即可;斜率存在时,设直线方程,联立方程组,利用韦达定理表示出![]() ,和
,和![]() ,借助向量的坐标运算,求出
,借助向量的坐标运算,求出![]() 为锐角,进而判断出
为锐角,进而判断出![]() 与以
与以![]() 为直径的圆的位置关系.
为直径的圆的位置关系.
(1)![]()
![]() ,点
,点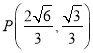 在
在![]() 上,
上,
可得![]() ,即
,即![]() ,
,![]() ,解得
,解得![]() ,
,
则椭圆的方程为![]() ;
;
(2)当直线![]() 的斜率不存在时,设直线方程为
的斜率不存在时,设直线方程为![]() 和
和![]() ,
,
若![]() ,可得与椭圆的交点为
,可得与椭圆的交点为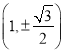 ,
,
以![]() 为直径的圆心为
为直径的圆心为![]() ,半径为
,半径为![]() ,
,![]() ,即
,即![]() 在圆外;
在圆外;
同理可得![]() 时,也有
时,也有![]() 在圆外;
在圆外;
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,
则![]() 到
到![]() 的距离为
的距离为![]() ,即
,即![]() ,
,
联立椭圆方程和直线l的方程可得![]() ,
,
![]() ,
,
设![]() ,
,![]() ,即有
,即有![]() ,
,![]() ,
,
![]()
![]() ,
,
即![]() ,则
,则![]() 为锐角,故
为锐角,故![]() 在以
在以![]() 为直径的圆外.
为直径的圆外.
综上可得,![]() 在以
在以![]() 为直径的圆外.
为直径的圆外.

【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取![]() 名工人,将他们随机分成两组,每组
名工人,将他们随机分成两组,每组![]() 人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:
人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:![]() )绘制了如图所示的茎叶图(茎为十位数,叶为个位数):
)绘制了如图所示的茎叶图(茎为十位数,叶为个位数):
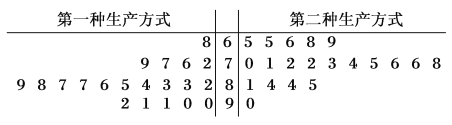
(1)根据茎叶图,估计两种生产方式完成任务所需时间至少![]() 分钟的概率,并对比两种生产方式所求概率,判断哪种生产方式的效率更高?
分钟的概率,并对比两种生产方式所求概率,判断哪种生产方式的效率更高?
(2)将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有![]() 的把握认为两种生产方式的效率有差异?
的把握认为两种生产方式的效率有差异?
附: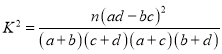
|
|
|
|
|
|
|
|