题目内容
【题目】已知函数![]() .
.
(1)当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的最小值;
的最小值;
(2)设数列![]() ,其前
,其前![]() 项和为
项和为![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)![]() ,分
,分![]() ,
,![]() ,
,![]() 三种情况推理即可;
三种情况推理即可;
(2)由(1)可得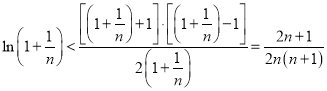 ,即
,即![]() ,利用累加法即可得到证明.
,利用累加法即可得到证明.
(1)由![]() ,得
,得![]() .
.
当![]() 时,方程
时,方程![]() 的
的![]() ,因此
,因此![]() 在区间
在区间![]()
上恒为负数.所以![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递减.
上单调递减.
又![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上恒成立;
上恒成立;
当![]() 时,方程
时,方程![]() 有两个不等实根,且满足
有两个不等实根,且满足![]() ,
,
所以函数![]() 的导函数
的导函数![]() 在区间
在区间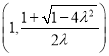 上大于零,函数
上大于零,函数![]() 在区间
在区间
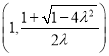 上单增,又
上单增,又![]() ,所以函数
,所以函数![]() 在区间
在区间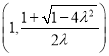 上恒大于零,不满足题意;
上恒大于零,不满足题意;
当![]() 时,在区间
时,在区间![]() 上
上![]() ,函数
,函数![]() 在区间
在区间![]()
上恒为正数,所以在区间![]() 上
上![]() 恒为正数,不满足题意;
恒为正数,不满足题意;
综上可知:若![]() 时,不等式
时,不等式![]() 恒成立,
恒成立,![]() 的最小值为
的最小值为![]() .
.
(2)由第(1)知:若![]() 时,
时,![]() .
.
若![]() ,则
,则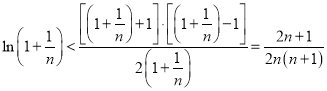 ,
,
即![]() 成立.
成立.
将![]() 换成
换成![]() ,得
,得![]() 成立,即
成立,即
![]() ,
,
以此类推,得![]() ,
,
![]() ,
,
上述各式相加,得![]() ,
,
又![]() ,所以
,所以![]() .
.

练习册系列答案
相关题目
【题目】根据国家统计局数据,1978年至2018年我国GDP总量从0.37万亿元跃升至90万亿元,实际增长了242倍多,综合国力大幅提升.
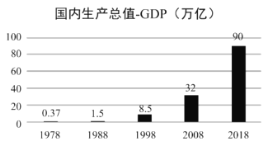
将年份1978,1988,1998,2008,2018分别用1,2,3,4,5代替,并表示为![]() ;
;![]() 表示全国GDP总量,表中
表示全国GDP总量,表中![]() ,
,![]() .
.
|
|
|
|
|
|
3 | 26.474 | 1.903 | 10 | 209.76 | 14.05 |
(1)根据数据及统计图表,判断![]() 与
与![]() (其中
(其中![]() 为自然对数的底数)哪一个更适宜作为全国GDP总量
为自然对数的底数)哪一个更适宜作为全国GDP总量![]() 关于
关于![]() 的回归方程类型?(给出判断即可,不必说明理由),并求出
的回归方程类型?(给出判断即可,不必说明理由),并求出![]() 关于
关于![]() 的回归方程.
的回归方程.
(2)使用参考数据,估计2020年的全国GDP总量.
线性回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
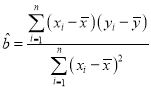 ,
,![]() .
.
参考数据:
| 4 | 5 | 6 | 7 | 8 |
| 55 | 148 | 403 | 1097 | 2981 |