题目内容
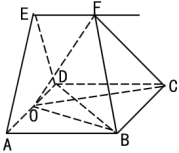
【题目】已知正四棱柱
的底面边长
,侧棱长
,它的外接球的球心为
，点
是
的中点，点
是球上的任意一点，有以下命题：
①
的长的最大值为9;
②三棱锥
的体积的最大值是
;
③存在过点的平面，截球的截面面积为
;
④三棱锥
的体积的最大值为20；
⑤过点的平面截球所得的截面面积最大时，
垂直于该截面.
其中是真命题的序号是___________
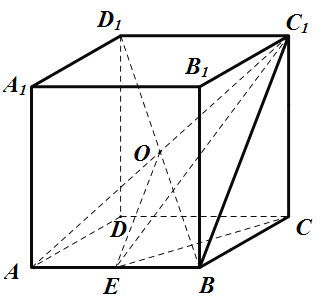
【答案】①③④
【解析】
计算外接球半径为
，
，得到①正确；三棱锥
的
，计算得到②错误；当截面与
垂直时，
，故③正确；三棱锥
，
，计算得到④；根据
得到⑤错误，得到答案.
外接球半径为：
，
，
故
的最大值为
，①正确；
，高
，故
，②错误；
当截面与垂直时，
，故，故③正确；
，，故
，故④正确；
当过点
的平面截球
所得的截面面积最大时，截面过直线，，故⑤错误.
故答案为：①③④.
练习册系列答案
相关题目
【题目】第七届世界军人运动会于2019年10月18日至2019年10月27日在中国武汉举行，第七届世界军人运动会是我国第一次承办的综合性国际军事体育赛事，也是继北京奥运会之后我国举办的规模最大的国际体育盛会.来自109个国家的9300余名军体健儿在江城武汉同场竞技、增进友谊.运动会共设置射击、游泳、田径、篮球等27个大项、329个小项.经过激烈角逐，奖牌榜的前6名如下：
某大学德语系同学利用分层抽样的方式从德国获奖选手中抽取了9名获奖代表.
国家 | 金牌 | 银牌 | 铜牌 | 奖牌总数 |
中国 | 133 | 64 | 42 | 239 |
俄罗斯 | 51 | 53 | 57 | 161 |
巴西 | 21 | 31 | 36 | 88 |
法国 | 13 | 20 | 24 | 57 |
波兰 | 11 | 15 | 34 | 60 |
德国 | 10 | 15 | 20 | 45 |
（1）请问这9名获奖代表中获金牌、银牌、铜牌的人数分别是多少人？
，求的分布列和期望；（3）从这9人中随机抽取3人，求已知这3人中有获金牌运动员的前提下，这3人中恰好有1人为获铜牌运动员的概率.
